题目内容
已知E，F分别为正方体ABCD-A1B1C1D的棱AB，AA1上的点，且AE=
AB，AF=
AA1，M，N分别为线段D1E和线段C1F上的点，则与平面ABCD平行的直线MN有（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| A、1条 | B、3条 | C、6条 | D、无数条 |
考点：直线与平面平行的性质
专题：空间位置关系与距离
分析：取BH=
BB1，连接FH，在D1E上任取一点M，过M在面D1HE中，作MG平行于HO，其中O满足线段OE=
D1E，再过G作GN∥FH，交C1F于N，连接MN，根据线面平行的判定定理，得到GM∥平面ABCD，NG∥平面ABCD，再根据面面平行的判断定理得到平面MNG∥平面ABCD，由面面平行的性质得到则MN∥平面ABCD，由于M是任意的，故MN有无数条．
| 1 |
| 3 |
| 1 |
| 3 |
解答：
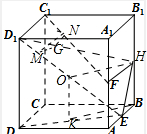解：取BH=
BB1，连接FH，则FH∥C1D
连接HE，在D1E上任取一点M，
过M在面D1HE中，作MG∥HO，交D1H于G，
其中O为线段OE=
D1E
再过G作GN∥FH，交C1F于N，连接MN，
由于GM∥HO，HO∥KB，KB?平面ABCD，
GM?平面ABCD，
所以GM∥平面ABCD，
同理由NG∥FH，可推得NG∥平面ABCD，
由面面平行的判定定理得，平面MNG∥平面ABCD，
则MN∥平面ABCD．
由于M为D1E上任一点，故这样的直线MN有无数条．
故选D．
解：取BH=| 1 |
| 3 |
连接HE，在D1E上任取一点M，
过M在面D1HE中，作MG∥HO，交D1H于G，
其中O为线段OE=
| 1 |
| 3 |
再过G作GN∥FH，交C1F于N，连接MN，
由于GM∥HO，HO∥KB，KB?平面ABCD，
GM?平面ABCD，
所以GM∥平面ABCD，
同理由NG∥FH，可推得NG∥平面ABCD，
由面面平行的判定定理得，平面MNG∥平面ABCD，
则MN∥平面ABCD．
由于M为D1E上任一点，故这样的直线MN有无数条．
故选D．
点评：本题考查空间直线与平面的位置关系，主要是直线与平面平行的判断和面面平行的判定与性质，考查空间想象能力和简单推理能力．
练习册系列答案
相关题目
设复数z=
，则z=（ ）
| 2-i |
| 1+i |
A、
| ||||
B、
| ||||
| C、1-3i | ||||
| D、1+3i |
已知集合A={x|y=lnx}，集合B={-2，-1，0，1，2}，则A∩B=（ ）
| A、（0，2） |
| B、{1，2} |
| C、（0，2） |
| D、{0，1，2} |