题目内容
已知数列{an}的前n项和为Sn且Sn=2n2+n,n∈N*,数列{bn}满足an=4log2bn+3,n∈N*.
(Ⅰ)求an和bn的通项公式;
(Ⅱ)求数列{an•bn}的前n项和Tn.
(Ⅰ)求an和bn的通项公式;
(Ⅱ)求数列{an•bn}的前n项和Tn.
考点:数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)首先根据递推关系式求出数列an的通项公式,进一步利用an的通项公式求出数列bn的通项公式.
(Ⅱ)根据(Ⅰ)的结论,求出新数列的通项公式,进一步利用乘公比错位相减法求出数列的前n项和.
(Ⅱ)根据(Ⅰ)的结论,求出新数列的通项公式,进一步利用乘公比错位相减法求出数列的前n项和.
解答:
解:(Ⅰ)数列{an}的前n项和为Sn且Sn=2n2+n,n∈N*,
则:an=Sn-Sn-1(n≥2),
=2n2+n-2(n-1)2-(n-1)
=4n-1,
当n=1时,a1=3符合通项公式,
所以:an=4n-1.
由于:数列{bn}满足an=4log2bn+3,n∈N*.
则:4n-1=4log2bn+3,
所以:bn=2n-1,
(Ⅱ)由(Ⅰ)得:设cn=anbn=(4n-1)2n-1,
则:Tn=c1+c2+…+cn=3•20+7•21+…+(4n-1)2n-1①
2Tn=3•21+7•22+…+(4n-1)2n②
①-②得:-Tn=4(20+21+…+2n-1)-(4n-1)2n-1,
整理得:Tn=(4n-5)2n+5.
则:an=Sn-Sn-1(n≥2),
=2n2+n-2(n-1)2-(n-1)
=4n-1,
当n=1时,a1=3符合通项公式,
所以:an=4n-1.
由于:数列{bn}满足an=4log2bn+3,n∈N*.
则:4n-1=4log2bn+3,
所以:bn=2n-1,
(Ⅱ)由(Ⅰ)得:设cn=anbn=(4n-1)2n-1,
则:Tn=c1+c2+…+cn=3•20+7•21+…+(4n-1)2n-1①
2Tn=3•21+7•22+…+(4n-1)2n②
①-②得:-Tn=4(20+21+…+2n-1)-(4n-1)2n-1,
整理得:Tn=(4n-5)2n+5.
点评:本题考查的知识要点:等差与等比数列通项公式的求法,乘公比错位相减法的应用.属于基础题型.

练习册系列答案
相关题目
已知两条不同的直线m,n和两个不同的平面α,β,以下四个结论中正确的个数为( )
①若m∥α,n∥β,且α∥β,则m∥n;
②若m∥α,n⊥β,且α⊥β,则m∥n;
③若m⊥α,n∥β,且α∥β,则m⊥n;
④若m⊥α,n⊥β,且α⊥β,则m⊥n.
①若m∥α,n∥β,且α∥β,则m∥n;
②若m∥α,n⊥β,且α⊥β,则m∥n;
③若m⊥α,n∥β,且α∥β,则m⊥n;
④若m⊥α,n⊥β,且α⊥β,则m⊥n.
| A、1个 | B、2个 | C、3个 | D、4个 |
在△ABC中,若S△ABC=
(a2+b2-c2),那么C等于( )
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若函数f(x)=x2+bx+1在区间(0,1)和(1,2)上各有一个零点,则b的取值范围是( )
| A、(-∞,-2) | ||
B、(-
| ||
C、(-
| ||
D、(-∞,-
|
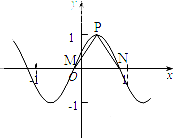 已知函数f(x)=
已知函数f(x)=
| ||
| 2 |
| 1 |
| 2 |
| PM |
| PN |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=
为偶函数,则括号内应该填写的是( )
|
| A、x2+3x-2 |
| B、x2-3x-2 |
| C、-x2+3x-2 |
| D、-x2+3x+2 |