ЬтФПФкШн
ФГжжВЈЕФДЋВЅЪЧгЩЧњЯпfЃЈxЃЉ=AsinЃЈІиx+ІеЃЉЃЈAЃО0ЃЉРДЪЕЯжЕФЃЌЮвУЧАбКЏЪ§НтЮіЪНfЃЈxЃЉ=AsinЃЈІиx+ІеЃЉГЦЮЊЁАВЈЁБЃЌАбеёЗљЖМЪЧA ЕФВЈГЦЮЊЁАAРрВЈЁБЃЌАбСНИіНтЮіЪНЯрМгГЦЮЊВЈЕФЕўМгЃЎ
ЃЈ1ЃЉвбжЊЁА1 РрВЈЁБжаЕФСНИіВЈf1ЃЈxЃЉ=sinЃЈx+Іе1ЃЉгыf2ЃЈxЃЉ=sinЃЈx+Іе2ЃЉЕўМгКѓШдЪЧЁА1РрВЈЁБЃЌЧѓІе2-Іе1ЕФжЕЃЛ
ЃЈ2ЃЉдкЁАAРрВЈЁАжагавЛИіЪЧf1ЃЈxЃЉ=sinxЃЌДг AРрВЈжадйевГіСНИіВЛЭЌЕФВЈЃЈУПСНИіВЈЕФГѕЯрІеЖМВЛЭЌЃЉЪЙЕУетШ§ИіВЛЭЌЕФВЈЕўМгжЎКѓЪЧЁАЦНВЈЁБЃЌМДЕўМгКѓy=0ЃЌВЂЫЕУїРэгЩЃЎ
ЃЈ1ЃЉвбжЊЁА1 РрВЈЁБжаЕФСНИіВЈf1ЃЈxЃЉ=sinЃЈx+Іе1ЃЉгыf2ЃЈxЃЉ=sinЃЈx+Іе2ЃЉЕўМгКѓШдЪЧЁА1РрВЈЁБЃЌЧѓІе2-Іе1ЕФжЕЃЛ
ЃЈ2ЃЉдкЁАAРрВЈЁАжагавЛИіЪЧf1ЃЈxЃЉ=sinxЃЌДг AРрВЈжадйевГіСНИіВЛЭЌЕФВЈЃЈУПСНИіВЈЕФГѕЯрІеЖМВЛЭЌЃЉЪЙЕУетШ§ИіВЛЭЌЕФВЈЕўМгжЎКѓЪЧЁАЦНВЈЁБЃЌМДЕўМгКѓy=0ЃЌВЂЫЕУїРэгЩЃЎ
ПМЕуЃКШ§НЧКЏЪ§жаЕФКуЕШБфЛЛгІгУ,СННЧКЭгыВюЕФе§ЯвКЏЪ§
зЈЬтЃКШ§НЧКЏЪ§ЕФЧѓжЕ,Ш§НЧКЏЪ§ЕФЭМЯёгыаджЪ
ЗжЮіЃКЃЈ1ЃЉЪзЯШЖдКЏЪ§ЕФЙиЯЕЪННјааКуЕШБфЛЛНјвЛВНЧѓГіКЏЪ§жаНЧЕФДѓаЁЃЎ
ЃЈ2ЃЉРћгУЃЈ1ЃЉЕФНсТлдйЖдКЏЪ§ЙиЯЕЪННјааБфЛЛзюКѓжЄУїГіКЏЪ§ЪБЦНВЈЃЎ
ЃЈ2ЃЉРћгУЃЈ1ЃЉЕФНсТлдйЖдКЏЪ§ЙиЯЕЪННјааБфЛЛзюКѓжЄУїГіКЏЪ§ЪБЦНВЈЃЎ
НтД№ЃК
НтЃКЃЈ1ЃЉf1ЃЈxЃЉ+f2ЃЈxЃЉ=sinЃЈx+ІЕ1ЃЉ+sinЃЈx+ІЕ2ЃЉ
=ЃЈcosІЕ1+cosІЕ2ЃЉsinx+ЃЈsinІЕ1+sinІЕ2ЃЉcosxІЕ
ЫљвдКЏЪ§ЕФеёЗљЮЊЃК
=
дђЃК
=1
МДЃКcos(ІЕ 1-ІЕ2)=-
ЫљвдЃКІЕ 1-ІЕ 2=2kІаЁР
ЃЈkЁЪZЃЉ
ЃЈ2ЃЉЩшf2ЃЈxЃЉ=AsinЃЈx+ІЕ1ЃЉЃЌf3ЃЈxЃЉ=AsinЃЈx+ІЕ2ЃЉ
дђЃК
f1ЃЈxЃЉ+f2ЃЈxЃЉ+f3ЃЈxЃЉ
=Asinx+AsinЃЈx+ІЕ1ЃЉ+AsinЃЈx+ІЕ2ЃЉ
=AsinxЃЈ1+cosІЕ1+cosІЕ2ЃЉ+AcosxЃЈsinІЕ1+sinІЕ2ЃЉ=0КуГЩСЂЃЎ
дђЃК
МДЃК
ЯћШЅІЕ2
ЕУЕНЃКcosІЕ 1=-
ШєШЁІЕ1=
ЃЌдђПЩШЁІЕ2=
ДЫЪБЃКf2(x)=Asin(x+
)ЃЌf3(x)=Asin(x+
)
f1ЃЈxЃЉ+f2ЃЈxЃЉ+f3ЃЈxЃЉ
=A(sinx+(-
sinx+
cosx)+(-
sinx-
cosx))=0=0
ЫљвдЮЊЦНВЈЃЎ
=ЃЈcosІЕ1+cosІЕ2ЃЉsinx+ЃЈsinІЕ1+sinІЕ2ЃЉcosxІЕ
ЫљвдКЏЪ§ЕФеёЗљЮЊЃК
| (cosІЕ1+cosІЕ2)2+(sinІЕ1+sinІЕ 2)2 |
| 2+2cos(ІЕ 1-ІЕ 2) |
дђЃК
| 2+2cos(ІЕ 1-ІЕ 2) |
МДЃКcos(ІЕ 1-ІЕ2)=-
| 1 |
| 2 |
ЫљвдЃКІЕ 1-ІЕ 2=2kІаЁР
| 2Іа |
| 3 |
ЃЈ2ЃЉЩшf2ЃЈxЃЉ=AsinЃЈx+ІЕ1ЃЉЃЌf3ЃЈxЃЉ=AsinЃЈx+ІЕ2ЃЉ
дђЃК
f1ЃЈxЃЉ+f2ЃЈxЃЉ+f3ЃЈxЃЉ
=Asinx+AsinЃЈx+ІЕ1ЃЉ+AsinЃЈx+ІЕ2ЃЉ
=AsinxЃЈ1+cosІЕ1+cosІЕ2ЃЉ+AcosxЃЈsinІЕ1+sinІЕ2ЃЉ=0КуГЩСЂЃЎ
дђЃК
|
МДЃК
|
ЯћШЅІЕ2
ЕУЕНЃКcosІЕ 1=-
| 1 |
| 2 |
ШєШЁІЕ1=
| 2Іа |
| 3 |
| 4Іа |
| 3 |
ДЫЪБЃКf2(x)=Asin(x+
| 2Іа |
| 3 |
| 4Іа |
| 3 |
f1ЃЈxЃЉ+f2ЃЈxЃЉ+f3ЃЈxЃЉ
=A(sinx+(-
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
ЫљвдЮЊЦНВЈЃЎ
ЕуЦРЃКБОЬтПМВщЕФжЊЪЖвЊЕуЃКШ§НЧКЏЪ§ЙиЯЕЪНЕФКуЕШБфЛЛЃЌаХЯЂЬтЕФгІгУЃЌжївЊПМВщбЇЩњЖдЪЕМЪЮЪЬтЕФгІгУФмСІЃЌЪєгкжаЕЕЬтаЭЃЎ

СЗЯАВсЯЕСаД№АИ
ЯрЙиЬтФП
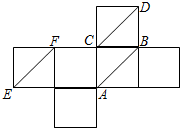
ШчЭМЪЧе§ЗНЬхЕФЦНУцеЙПЊЭМЃЌдкетИіе§ЗНЬхжаЃЌе§ШЗЕФУќЬтЪЧЃЈЁЁЁЁЃЉ

| AЁЂBDгыCFГЩ60ЁуНЧ |
| BЁЂBDгыEFГЩ60ЁуНЧ |
| CЁЂABгыCDГЩ60ЁуНЧ |
| DЁЂABгыEFГЩ60ЁуНЧ |
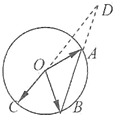 ШчЭМЫљЪОЃЌAЃЌBЃЌCЪЧдВOЩЯЕФШ§ЕуЃЌCOЕФбгГЄЯпгыЯпЖЮBAЕФбгГЄЯпНЛгкдВЭтЕФЕуDЃЌШє
ШчЭМЫљЪОЃЌAЃЌBЃЌCЪЧдВOЩЯЕФШ§ЕуЃЌCOЕФбгГЄЯпгыЯпЖЮBAЕФбгГЄЯпНЛгкдВЭтЕФЕуDЃЌШє| OC |
| OA |
| OB |
| AЁЂЃЈ1ЃЌ+ЁоЃЉ |
| BЁЂЃЈ-ЁоЃЌ-1ЃЉ |
| CЁЂЃЈ0ЃЌ1ЃЉ |
| DЁЂЃЈ-1ЃЌ0ЃЉ |