题目内容
求直线l1:x-y+1=0关于直线l:y=-x对称直线l2的方程.
考点:与直线关于点、直线对称的直线方程
专题:计算题,直线与圆
分析:先求得直线l与直线l1的交点A的坐标,在直线l1上取一点C(0,1),求出点C关于直线l对称点B的坐标,
可得AB的斜率,用点斜式求得对称直线l2的方程.
可得AB的斜率,用点斜式求得对称直线l2的方程.
解答:
解:由
,解得
,
即有l1和l的交点A为(-
,
),
再在l1上取一点C(0,1),则点C关于直线l对称点B(m,n),
则有
,解得
,
故点B(-1,0),
故AB的斜率为 KAB=
=1,
由点斜式求得直线l1关于直线l对称的直线AB
即直线l2的方程为 y=x+1.
|
|
即有l1和l的交点A为(-
| 1 |
| 2 |
| 1 |
| 2 |
再在l1上取一点C(0,1),则点C关于直线l对称点B(m,n),
则有
|
|
故点B(-1,0),
故AB的斜率为 KAB=
| ||
-
|
由点斜式求得直线l1关于直线l对称的直线AB
即直线l2的方程为 y=x+1.
点评:本题考查直线的对称问题,考查直线关于直线对称的问题,注意转化为一个点关于某直线的对称点的坐标的方法,用点斜式求直线的方程的问题,属于中档题.

练习册系列答案
相关题目
若函数f(x)为定义在R上的奇函数,且在(0,+∞)内是增函数,又f(2)=0,则不等式xf(x)<0的解集为( )
| A、(-2,0)∪(2,+∞) |
| B、(-∞,-2)∪(0,2) |
| C、(-∞,-2)∪(2,+∞) |
| D、(-2,0)∪(0,2) |
若sin2t=-
cosxdx,其中t∈(0,π),则t=( )
| ∫ | π 0 |
A、
| ||
B、
| ||
C、
| ||
| D、π |
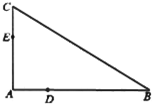 如图,D,E分别为△ABC的边AB,AC上的点,且不与△ABC的顶点重合,已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程x2-14x-mn=0的两个根.
如图,D,E分别为△ABC的边AB,AC上的点,且不与△ABC的顶点重合,已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程x2-14x-mn=0的两个根. 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.