题目内容
1.已知等差数列{an}与等差数列{bn}的前n项和分别为Sn和Tn,若$\frac{S_n}{T_n}=\frac{3n-1}{2n+3}$,则$\frac{{{a_{10}}}}{{{b_{10}}}}$=( )| A. | $\frac{3}{2}$ | B. | $\frac{14}{13}$ | C. | $\frac{56}{41}$ | D. | $\frac{29}{23}$ |
分析 由等差数列的求和公式和性质可得$\frac{{{a_{10}}}}{{{b_{10}}}}$=$\frac{{a}_{1}+{a}_{19}}{{b}_{1}+{b}_{19}}$=$\frac{{S}_{19}}{{T}_{19}}$,代值计算可得.
解答 解:由等差数列的求和公式和性质可得$\frac{{{a_{10}}}}{{{b_{10}}}}$=$\frac{{a}_{1}+{a}_{19}}{{b}_{1}+{b}_{19}}$=$\frac{{S}_{19}}{{T}_{19}}$=$\frac{56}{41}$.
故选C.
点评 本题考查等差数列的求和公式和等差数列的性质,属基础题.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
10.已知椭圆与双曲线$\frac{x^2}{3}-\frac{y^2}{2}=1$有共同的焦点,且离心率为$\frac{{\sqrt{5}}}{5}$,则椭圆的标准方程为( )
| A. | $\frac{x^2}{20}+\frac{y^2}{25}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{5}=1$ | C. | $\frac{x^2}{25}+\frac{y^2}{20}=1$ | D. | $\frac{x^2}{5}+\frac{y^2}{25}=1$ |
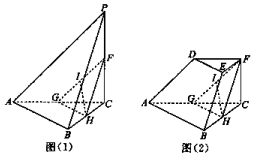 如图(1),三棱锥P-ABC中,PC⊥平面ABC,F,G,H,分别是PC,AC,BC的中点,I是线段FG上任意一点,PC=AB=2BC,过点F作平行于底面ABC的平面截三棱锥,得到几何体DEF-ABC,如图(2)所示.
如图(1),三棱锥P-ABC中,PC⊥平面ABC,F,G,H,分别是PC,AC,BC的中点,I是线段FG上任意一点,PC=AB=2BC,过点F作平行于底面ABC的平面截三棱锥,得到几何体DEF-ABC,如图(2)所示.