题目内容
11.过原点O作圆x2+y2-8x=0的弦OA,延长OA到N,使|OA|=|AN|,求点N的轨迹方程.分析 设N(x,y),延长OA到N,使|OA|=|AN|,可得A$(\frac{x}{2},\frac{y}{2})$.由于点A在圆(x′)2+(y′)2-8x′=0上,即可得出.
解答 解:设N(x,y),∵延长OA到N,使|OA|=|AN|,∴A$(\frac{x}{2},\frac{y}{2})$.
由于点A在圆(x′)2+(y′)2-8x′=0上,
∴$(\frac{x}{2})^{2}+(\frac{y}{2})^{2}$-8×$\frac{x}{2}$=0,化为:x2+y2-16x=0,即为点N的轨迹方程.
点评 本题考查了圆的方程、中点坐标公式、“代点法”,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
2.函数y=sin(2x+$\frac{π}{3}$ )的一条对称轴为( )
| A. | x=$\frac{π}{2}$ | B. | x=0 | C. | x=-$\frac{π}{6}$ | D. | x=$\frac{π}{12}$ |
16.设集合A={x|1<x<2},B={x|x<a}满足A?B,则实数a的取值范围是( )
| A. | [2,+∞) | B. | (-∞,1] | C. | [1,+∞) | D. | (-∞,2] |
3.以椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$的中心为原点,左焦点为焦点的抛物线的标准方程是( )
| A. | x2=8y | B. | y2=16x | C. | x2=-8y | D. | y2=-16x |
1.已知等差数列{an}与等差数列{bn}的前n项和分别为Sn和Tn,若$\frac{S_n}{T_n}=\frac{3n-1}{2n+3}$,则$\frac{{{a_{10}}}}{{{b_{10}}}}$=( )
| A. | $\frac{3}{2}$ | B. | $\frac{14}{13}$ | C. | $\frac{56}{41}$ | D. | $\frac{29}{23}$ |
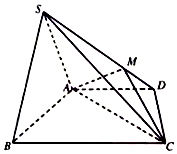 如图,在四棱锥S-ABCD中,底面梯形ABCD中,AD∥BC,平面SAB⊥平面ABCD,△SAB是等边三角形,已知$AC=2AB=4,BC=2AD=2CD=2\sqrt{5}$,M是SD上任意一点,$\overrightarrow{SM}=m\overrightarrow{MD}$,且m>0.
如图,在四棱锥S-ABCD中,底面梯形ABCD中,AD∥BC,平面SAB⊥平面ABCD,△SAB是等边三角形,已知$AC=2AB=4,BC=2AD=2CD=2\sqrt{5}$,M是SD上任意一点,$\overrightarrow{SM}=m\overrightarrow{MD}$,且m>0.