题目内容
已知函数f(x)=
+
的两个极值点x1,x2,且x1,x2分别是一个椭圆和一个双曲线的离心率,点P(m,n)表示的平面区域为D,若函数y=ax+4-7(a>1)的图象存在区域D内的点,则实数a的取值范围是( )
| x3 |
| 3 |
| mx2+(m+n)x+1 |
| 2 |
| A、(2,+∞) |
| B、[2,+∞) |
| C、[1,2] |
| D、(1,2) |
考点:利用导数研究函数的极值
专题:综合题,导数的综合应用
分析:根据极值的意义可知,极值点x1、x2是导函数等于零的两个根,可得方程x2+mx+
(m+n)=0的两根,一根属于(0,1),另一根属于(1,+∞),从而可确定平面区域为D,进而利用函数y=ax+4-7(a>1)的图象存在区域D内的,可求实数a的取值范围.
| 1 |
| 2 |
解答:
解:求导函数可得y'=x2+mx+
(m+n),
依题意知,方程y'=0有两个根x1、x2,且x1∈(0,1),x2∈(1,+∞),
构造函数f(x)=x2+mx+
(m+n),
∴
,∴
,
∵直线m+n=0,2+3m+n=0的交点坐标为(-1,1)
∴要使函数y=ax+4-7(a>1)的图象存在区域D内的点,则必须满足1<a-1+4-7,
∴a3<8,解得a>2,
故选A.
| 1 |
| 2 |
依题意知,方程y'=0有两个根x1、x2,且x1∈(0,1),x2∈(1,+∞),
构造函数f(x)=x2+mx+
| 1 |
| 2 |
∴
|
|
∵直线m+n=0,2+3m+n=0的交点坐标为(-1,1)
∴要使函数y=ax+4-7(a>1)的图象存在区域D内的点,则必须满足1<a-1+4-7,
∴a3<8,解得a>2,
故选A.
点评:本题主要考查了利用导数研究函数的极值,以及二元一次不等式(组)与平面区域,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知x、y满足条件
,若目标函数z=ax+y取得最大值时的最优解有无数个,则实数a的值为( )
|
A、-
| ||
B、-
| ||
C、
| ||
D、
|
已知函数f(x)=(
)x-log2x,若x0是函数y=f(x)的零点,且0<x1<x0,则有( )
| 1 |
| 3 |
| A、f(x1)>0 |
| B、f(x1)<0 |
| C、f(x1)=0 |
| D、f(x1)>0与f(x1)<0均有可能 |
若a∈R,则复数z=
对应的点不可能在复平面的( )
| a+i |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
设p、q是简单命题,则“p∧q为真”是“p∨q为真”的( )
| A、充分但不必要条件 |
| B、必要但不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知函数y=sin(ωx+φ)(ω>0,-
<φ<
)的部分图象如图所示,则( )
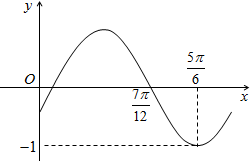
| π |
| 2 |
| π |
| 2 |

A、ω=2,φ=-
| ||
B、ω=2,φ=
| ||
C、ω=1,φ=-
| ||
D、ω=1,φ=
|