题目内容
某校有5名同学参加A、B、C三所学校的自主招生考试,每人限报一所高校,若这三所学校中每个学校都至少有1名同学报考,那么这5名同学不同的报考方法种数共有 种.(用数字作答)
考点:排列、组合及简单计数问题
专题:计算题,排列组合
分析:由题设条件知,可以把学生分成两类:311,221,所以共有
•
+
种报考方法.
| ||||
|
| A | 3 3 |
| ||||
|
解答:
解:把学生分成两类:311,221,
所以共有
•
+
•
=150种报考方法,
故答案为:150.
所以共有
| ||||
|
| A | 3 3 |
| ||||
|
| A | 3 3 |
故答案为:150.
点评:本题考查分类加法计数原理,解题时要认真审题,注意平均分组和不平均分组的合理运用.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
已知函数f(x)=
+
的两个极值点x1,x2,且x1,x2分别是一个椭圆和一个双曲线的离心率,点P(m,n)表示的平面区域为D,若函数y=ax+4-7(a>1)的图象存在区域D内的点,则实数a的取值范围是( )
| x3 |
| 3 |
| mx2+(m+n)x+1 |
| 2 |
| A、(2,+∞) |
| B、[2,+∞) |
| C、[1,2] |
| D、(1,2) |
在△ABC中,|
|=2,|
|=1,
•
=-1,则△ABC的外接圆半径是( )
| BA |
| AC |
| BA |
| AC |
| A、1 | ||||
| B、2 | ||||
C、
| ||||
D、
|

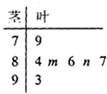 在某校举行的“校园艺术节”比赛上,七位评委为1号选手打出的分数的茎叶图如图所示,去掉一个最高分和一个最低分后,所剩数据的平均数为85,则m2+n2的最小值是
在某校举行的“校园艺术节”比赛上,七位评委为1号选手打出的分数的茎叶图如图所示,去掉一个最高分和一个最低分后,所剩数据的平均数为85,则m2+n2的最小值是