题目内容
试验:连续抛掷一粒般子(骸子每一面数字分别为1,2,3,4,5,6)两次,记向上数字依次为a,b,事件A:“函数f(x)=lg(x2+ax+b2)定义域为R”.事件B:“函数g(x)=(a-π)x是减函数(其中π是圆周率)”.
(1)分别写出事件A与事件B所含基本事件;
(2)求事件A+B与事件AB发生的概率.
(1)分别写出事件A与事件B所含基本事件;
(2)求事件A+B与事件AB发生的概率.
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(1)根据对数函数的定义域为R,则△=a2-4b2<0,再根据指数函数的单调性,求出a的值,用列举法表示出所有的可能;
(2)一次事件记为(a,b),则共有6×6=36种不同结果,因此共有36个基本事件,由件A+B含有29个基本事件,事件AB含有4个基本事件,代入概率公式即可求得结果.
(2)一次事件记为(a,b),则共有6×6=36种不同结果,因此共有36个基本事件,由件A+B含有29个基本事件,事件AB含有4个基本事件,代入概率公式即可求得结果.
解答:
解:(1)∵事件A:“函数f(x)=lg(x2+ax+b2)定义域为R”.
∴△=a2-4b2<0,
即a<2b,
∴事件A“a<2b”,
∵事件B:“函数g(x)=(a-π)x是减函数(其中π是圆周率)”.
∴0<a-π<1,
∴a=4
事件A含有(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),
(2,2),(2,3),(2,4),(2,5),(2,6),
(3,2),(3,3),(3,4),(3,5),(3,6),
(4,3),(4,4),(4,5),(4,6),
(5,3),(5,4),(5,5),(5,6),
(6,4),(6,5),(6,6),
事件B含有(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),
(2)一次事件记为(a,b),则共有6×6=36种不同结果,因此共有36个基本事件,
由件A+B含有29个基本事件,事件AB含有4个基本事件,
故P(A+B)=
,P(AB)=
=
∴△=a2-4b2<0,
即a<2b,
∴事件A“a<2b”,
∵事件B:“函数g(x)=(a-π)x是减函数(其中π是圆周率)”.
∴0<a-π<1,
∴a=4
事件A含有(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),
(2,2),(2,3),(2,4),(2,5),(2,6),
(3,2),(3,3),(3,4),(3,5),(3,6),
(4,3),(4,4),(4,5),(4,6),
(5,3),(5,4),(5,5),(5,6),
(6,4),(6,5),(6,6),
事件B含有(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),
(2)一次事件记为(a,b),则共有6×6=36种不同结果,因此共有36个基本事件,
由件A+B含有29个基本事件,事件AB含有4个基本事件,
故P(A+B)=
| 29 |
| 36 |
| 4 |
| 36 |
| 1 |
| 9 |
点评:古典概型和几何概型是我们学习的两大概型,古典概型要求能够列举出所有事件和发生事件的个数,而不能列举的就是几何概型,本小题考查古典概型及其概率计算公式,考查概率的求法:属中档题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
下列曲线中离心率为
的是( )
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
化简:(sin
+cos
)2+2sin2(
-
)得( )
| α |
| 2 |
| α |
| 2 |
| π |
| 4 |
| α |
| 2 |
| A、2+sinα | ||||
B、2+
| ||||
| C、2 | ||||
D、2+
|
已知向量
,
是两个不共线的向量,若
=2
-
与
=
+λ
共线,则λ=( )
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
| A、2 | ||
| B、-2 | ||
C、-
| ||
D、
|
 自锐角△ABC的顶点A向边BC引垂线,垂足为D.在AD上任取一点H,直线BH交AC于点E,CH交AB于点F.
自锐角△ABC的顶点A向边BC引垂线,垂足为D.在AD上任取一点H,直线BH交AC于点E,CH交AB于点F.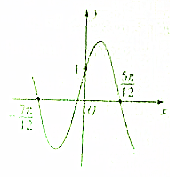 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<