题目内容
已知函数f(x)=lnx-
ax2-2x
(1)当a=1时,?x0∈[1,e],使不等式f(x0)≤m,求实数m的取值范围;
(2)若a=-
,且关于x的方程f(x)=-
x+b在[1,4]上恰有两个不等的实根,求实数b的取值范围;
(3)若在区间(1,+∞)上,函数f(x)的图象恒在直线y=2ax的下方,求实数a的取值范围.
| 1 |
| 2 |
(1)当a=1时,?x0∈[1,e],使不等式f(x0)≤m,求实数m的取值范围;
(2)若a=-
| 1 |
| 2 |
| 1 |
| 2 |
(3)若在区间(1,+∞)上,函数f(x)的图象恒在直线y=2ax的下方,求实数a的取值范围.
考点:导数在最大值、最小值问题中的应用,函数的零点与方程根的关系
专题:导数的综合应用
分析:(1)当a=1时,?x0∈[1,e],使不等式f(x0)≤m?m≥f(x)min,x∈[1,e].利用导数研究其单调性极值与最值即可得出.
(2)a=-
,关于x的方程f(x)=-
x+b化为lnx+
x2-
x-b=0,令g(x)=lnx+
x2-
x-b,x∈[1,4],利用导数研究其单调性极值与最值,可得:当x=2时,函数g(x)取得极小值即最小值,g(2)=ln2-2-b.而g(1)<g(4).由于关于x的方程f(x)=-
x+b在[1,4]上恰有两个不等的实根,可得g(2)<0,g(1)>0,解出即可.
(3)在区间(1,+∞)上,函数f(x)的图象恒在直线y=2ax的下方?f(x)<2ax.令h(x)=f(x)-2ax=lnx-
ax2-(2+2a)x,因此f(x)<2ax?h(x)max<0.h′(x)=
-ax-(2+2a)=
,对a分类讨论,利用导数研究函数h(x)的单调性极值与最值即可得出.
(2)a=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
(3)在区间(1,+∞)上,函数f(x)的图象恒在直线y=2ax的下方?f(x)<2ax.令h(x)=f(x)-2ax=lnx-
| 1 |
| 2 |
| 1 |
| x |
| -ax2-(2+2a)x+1 |
| x |
解答:
解:(1)当a=1时,?x0∈[1,e],使不等式f(x0)≤m?m≥f(x)min,x∈[1,e].
f′(x)=
-x-2=
=
<0,
∴函数f(x)在x∈[1,e]单调递减,
∴当x=e时,f(x)取得最小值f(e)=1-
e2-2e.
∴实数m的取值范围是[1-
e2-2e,+∞);
(2)a=-
,关于x的方程f(x)=-
x+b化为lnx+
x2-
x-b=0,
令g(x)=lnx+
x2-
x-b,x∈[1,4],
g′(x)=
+
x-
=
=
,
令g′(x)>0,解得2<x<4,此时函数g(x)单调递增;令g′(x)<0,解得1<x<2,此时函数g(x)单调递减.
∴当x=2时,函数g(x)取得极小值即最小值,g(2)=ln2-2-b.
而g(1)=-
-b,g(4)=2ln2-2-b,而g(4)-g(1)=2ln2-2+
=2ln2-
>0,∴g(1)<g(4).
∵关于x的方程f(x)=-
x+b在[1,4]上恰有两个不等的实根,
∴g(2)<0,g(1)>0,解得ln2-2<b≤-
.
∴实数b的取值范围是ln2-2<b≤-
.
(3)在区间(1,+∞)上,函数f(x)的图象恒在直线y=2ax的下方?f(x)<2ax.
令h(x)=f(x)-2ax=lnx-
ax2-(2+2a)x,因此f(x)<2ax?h(x)max<0.
h′(x)=
-ax-(2+2a)=
,
①a=0时,h′(x)=
<0,此时函数h(x)在(1,+∞)上单调递减,h(x)<h(1)=-2<0,满足条件;
②a≠0时,由△=(2+2a)2+4a<0时,解出
<a<
,
当
<a<
时,-a>0,∴h′(x)>0,
因此函数h(x)在(1,+∞)上单调递增,∴h(x)>h(1)=-
a-2-2a=-
-2,此时不满足h(x)max<0,舍去.
③a≠0时,由△=(2+2a)2+4a>0时,解得a>
或a<
,
当a<
时,-a>0,由h′(x)=0,x1+x2=-
<0,x1x2=
>0,∴x1,x2<0.
h′(x)=
>0,此时函数h(x)单调递增,舍去.
当a>0时,x1=
<0,x2=
<1,
当x>1时,h′(x)<0,此时函数h(x)单调递减,∴h(x)<h(1)=-
-2<0,满足题意.
当
<a<0时,x1x2>1,x1+x2>0,x2<1<x1.
∴函数h(x)在区间(1,x1)单调递减,在(x1,+∞)单调递增,舍去.
综上可得:实数a的取值范围是a≥0.
f′(x)=
| 1 |
| x |
| -(x2+2x-1) |
| x |
| -(x+1)2+2 |
| x |
∴函数f(x)在x∈[1,e]单调递减,
∴当x=e时,f(x)取得最小值f(e)=1-
| 1 |
| 2 |
∴实数m的取值范围是[1-
| 1 |
| 2 |
(2)a=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
令g(x)=lnx+
| 1 |
| 4 |
| 3 |
| 2 |
g′(x)=
| 1 |
| x |
| 1 |
| 2 |
| 3 |
| 2 |
| x2-3x+2 |
| 2x |
| (x-1)(x-2) |
| 2x |
令g′(x)>0,解得2<x<4,此时函数g(x)单调递增;令g′(x)<0,解得1<x<2,此时函数g(x)单调递减.
∴当x=2时,函数g(x)取得极小值即最小值,g(2)=ln2-2-b.
而g(1)=-
| 5 |
| 4 |
| 5 |
| 4 |
| 3 |
| 4 |
∵关于x的方程f(x)=-
| 1 |
| 2 |
∴g(2)<0,g(1)>0,解得ln2-2<b≤-
| 5 |
| 4 |
∴实数b的取值范围是ln2-2<b≤-
| 5 |
| 4 |
(3)在区间(1,+∞)上,函数f(x)的图象恒在直线y=2ax的下方?f(x)<2ax.
令h(x)=f(x)-2ax=lnx-
| 1 |
| 2 |
h′(x)=
| 1 |
| x |
| -ax2-(2+2a)x+1 |
| x |
①a=0时,h′(x)=
| -2x+1 |
| x |
②a≠0时,由△=(2+2a)2+4a<0时,解出
-3-
| ||
| 2 |
-3+
| ||
| 2 |
当
-3-
| ||
| 2 |
-3+
| ||
| 2 |
因此函数h(x)在(1,+∞)上单调递增,∴h(x)>h(1)=-
| 1 |
| 2 |
| 5a |
| 2 |
③a≠0时,由△=(2+2a)2+4a>0时,解得a>
-3+
| ||
| 2 |
-3-
| ||
| 2 |
当a<
-3-
| ||
| 2 |
| 2+2a |
| a |
| 1 |
| -a |
h′(x)=
| -a(x-x1)(x-x2) |
| x |
当a>0时,x1=
-(1+a)-
| ||
| a |
-(1+a)+
| ||
| a |
当x>1时,h′(x)<0,此时函数h(x)单调递减,∴h(x)<h(1)=-
| 5a |
| 2 |
当
-3+
| ||
| 2 |
∴函数h(x)在区间(1,x1)单调递减,在(x1,+∞)单调递增,舍去.
综上可得:实数a的取值范围是a≥0.
点评:本题考查了利用导数研究函数的单调性极值与最值值域及其函数的零点、一元二次方程的实数根与判别式的关系、根与系数的关系,考查了等价转化能力,考查了分类讨论的思想方法,考查了推理能力与计算能力,属于较难题.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
化简:(sin
+cos
)2+2sin2(
-
)得( )
| α |
| 2 |
| α |
| 2 |
| π |
| 4 |
| α |
| 2 |
| A、2+sinα | ||||
B、2+
| ||||
| C、2 | ||||
D、2+
|
过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于A,B,交其准线于点C,若
=-2
,|
|=3,则抛物线的方程为( )
| BC |
| BF |
| AF |
| A、y2=12x |
| B、y2=9x |
| C、y2=6x |
| D、y2=3x |
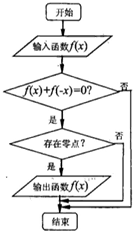
某程序框图如图所示,现输入如下四个函数,则可以输出的函数是( )

| A、f(x)=cosx | ||
B、f(x)=
| ||
| C、f(x)=lgx | ||
D、f(x)=
|
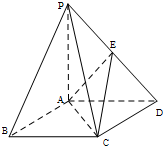 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,点E是PD的中点.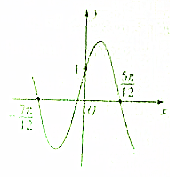 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<