题目内容
已知P是双曲线
-
=1(a>0,b>0)右支上一点,F1(-c,0),F2(c,0)分别是左、右焦点,则△PF1F2的内切圆圆心的横坐标为 .
| x2 |
| a2 |
| y2 |
| b2 |
考点:双曲线的简单性质
专题:计算题,数形结合,圆锥曲线的定义、性质与方程
分析:根据题意,利用切线长定理,再利用双曲线的定义,把|PF1|-|PF2|=2a,转化为|HF1|-|HF2|=2a,从而求得点H的横坐标.
解答:
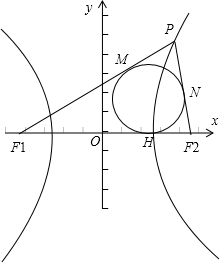 解:如图所示:F1(-a,0)、F2(a,0),
解:如图所示:F1(-a,0)、F2(a,0),
设内切圆与x轴的切点是点H,
PF1、PF2与内切圆的切点分别为M、N,
∵由双曲线的定义可得|PF1|-|PF2|=2a,
由圆的切线长定理知,|PM|=|PN|,故|MF1|-|NF2 |=2a,
即|HF1|-|HF2|=2a,
设内切圆的圆心横坐标为x,则点H的横坐标为x,
故 (x+c)-(c-x)=2a,∴x=a.
故答案为:a.
 解:如图所示:F1(-a,0)、F2(a,0),
解:如图所示:F1(-a,0)、F2(a,0),设内切圆与x轴的切点是点H,
PF1、PF2与内切圆的切点分别为M、N,
∵由双曲线的定义可得|PF1|-|PF2|=2a,
由圆的切线长定理知,|PM|=|PN|,故|MF1|-|NF2 |=2a,
即|HF1|-|HF2|=2a,
设内切圆的圆心横坐标为x,则点H的横坐标为x,
故 (x+c)-(c-x)=2a,∴x=a.
故答案为:a.
点评:本题考查双曲线的定义、切线长定理,体现了转化的数学思想以及数形结合的数学思想,正确运用双曲线的定义是关键

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于A,B,交其准线于点C,若
=-2
,|
|=3,则抛物线的方程为( )
| BC |
| BF |
| AF |
| A、y2=12x |
| B、y2=9x |
| C、y2=6x |
| D、y2=3x |
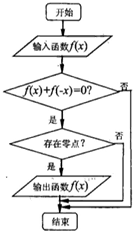
某程序框图如图所示,现输入如下四个函数,则可以输出的函数是( )

| A、f(x)=cosx | ||
B、f(x)=
| ||
| C、f(x)=lgx | ||
D、f(x)=
|
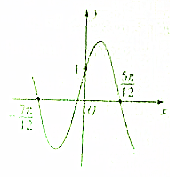 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<