题目内容
20.已知椭圆C:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的两个焦点为F1,F2,其离心率为$\frac{1}{2}$,点P是椭圆C上一点,若△PF1F2的面积为1且其内切圆的半径为$\frac{1}{3}$.(Ⅰ)求椭圆C的方程;
(Ⅱ)若点Q为椭圆C上异于长轴端点A1,A2的动点,定直线y=4与直线QA1、QA2分别相交于M、N两点,已知点G(0,7),试判断y轴上是否存在不同于点G的定点H,使得M,N,G,H四点共圆?若存在,求出点H的坐标;若不存在,请说明理由.
分析 (Ⅰ)运用椭圆的离心率公式和三角形的面积求法,结合内切圆的半径和椭圆的定义,解方程可得a,c,再由a,b,c的关系,可得b,进而得到椭圆方程;
(Ⅱ)设Q(m,n),可得$\frac{{m}^{2}}{3}$+$\frac{{n}^{2}}{4}$=1,A1(0,-2),A2(0,2),求得QA1,QA2的方程,代入y=4,可得M,N的坐标,求得圆心的横坐标,再由GM的中垂线经过圆心,可得圆心的纵坐标为定值4,即可得到H(0,1).
解答 解:(Ⅰ)由题意可得e=$\frac{c}{a}$=$\frac{1}{2}$,
${S}_{△P{F}_{1}{F}_{2}}$=$\frac{1}{2}$r(PF1+PF2+F1F2)=$\frac{1}{2}$×$\frac{1}{3}$(2a+2c)=1,
即为a+c=3,
解得c=1,a=2,b=$\sqrt{{a}^{2}-{c}^{2}}$=$\sqrt{3}$,
即有椭圆方程为$\frac{{y}^{2}}{4}$+$\frac{{x}^{2}}{3}$=1;
(Ⅱ)设Q(m,n),可得$\frac{{m}^{2}}{3}$+$\frac{{n}^{2}}{4}$=1,
A1(0,-2),A2(0,2),
直线QA1:y=$\frac{n+2}{m}$x-2,
直线QA2:y=$\frac{n-2}{m}$x+2,
令y=4,可得xM=$\frac{6m}{n+2}$;
xN=$\frac{2m}{n-2}$.
即有M($\frac{6m}{n+2}$,4),N($\frac{2m}{n-2}$,4),
由圆心在线段的垂直平分线上,可得
圆心的横坐标为$\frac{1}{2}$($\frac{6m}{n+2}$+$\frac{2m}{n-2}$)=$\frac{4m(n-1)}{{n}^{2}-4}$,
再由直线GM的斜率为$\frac{4-7}{\frac{6m}{n+2}}$=-$\frac{n+2}{2m}$,
可得线段GM的中垂线的斜率为$\frac{2m}{n+2}$,
GM的中点为($\frac{3m}{n+2}$,$\frac{11}{2}$),
可得GM的垂直平分线方程为y-$\frac{11}{2}$=$\frac{2m}{n+2}$(x-$\frac{3m}{n+2}$),
令x=$\frac{4m(n-1)}{{n}^{2}-4}$,可得y=$\frac{11}{2}$+$\frac{2m}{n+2}$•$\frac{mn+2m}{{n}^{2}-4}$
=$\frac{11}{2}$+$\frac{2{m}^{2}}{{n}^{2}-4}$=$\frac{11}{2}$+$\frac{3}{2}$•$\frac{4-{n}^{2}}{{n}^{2}-4}$=$\frac{11}{2}$-$\frac{3}{2}$=4.
即有圆心的纵坐标为定值4,
可得y轴上存在不同于点G的定点H(0,1),
使得M,N,G,H四点共圆.
点评 本题考查椭圆的方程的求法,注意运用离心率公式和三角形的内切圆的半径的求法,考查圆的方程的求法和运用,考查化简整理的运算能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 3 | B. | 2 | C. | 1 | D. | $\frac{1}{2}$ |
| A. | (1,$\frac{10}{3}$) | B. | (1,-$\frac{10}{3}$) | C. | (-1,-$\frac{10}{3}$) | D. | (-1,$\frac{10}{3}$) |
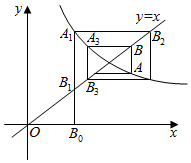 如图所示,折线B0A1B2A2B3A3…中线段分别平行于x轴或y轴,A1,A2,…,An…这些点在函数y=$\frac{2}{x-1}$(x>1)图象上,B1,B2…Bn…这些点在直线y=x上,设点An的纵坐标为yn.
如图所示,折线B0A1B2A2B3A3…中线段分别平行于x轴或y轴,A1,A2,…,An…这些点在函数y=$\frac{2}{x-1}$(x>1)图象上,B1,B2…Bn…这些点在直线y=x上,设点An的纵坐标为yn.