题目内容
11.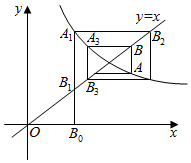 如图所示,折线B0A1B2A2B3A3…中线段分别平行于x轴或y轴,A1,A2,…,An…这些点在函数y=$\frac{2}{x-1}$(x>1)图象上,B1,B2…Bn…这些点在直线y=x上,设点An的纵坐标为yn.
如图所示,折线B0A1B2A2B3A3…中线段分别平行于x轴或y轴,A1,A2,…,An…这些点在函数y=$\frac{2}{x-1}$(x>1)图象上,B1,B2…Bn…这些点在直线y=x上,设点An的纵坐标为yn.(1)用yn表示yn+1(n∈N*);
(2)若B0($\frac{11}{5}$,0),请写出数列{yn}的所有项;
(3)设B0(x0,0),当x0为何值时,数列{yn}是一个无穷的常数列.
分析 (1)设B0(x0,0),由题意可得B1(x0,x0),B2($\frac{2}{{x}_{0}-1}$,$\frac{2}{{x}_{0}-1}$),B3($\frac{2}{\frac{2}{{x}_{0}-1}-1}$,$\frac{2}{\frac{2}{{x}_{0}-1}-1}$),即可得到所求关系式;
(2)由(1),运用列举法,即可得到所求数列中的所有项;
(3)由(1)可得,令yn+1=yn=t,(t>1),解方程即可得到所求值.
解答 解:(1)设B0(x0,0),由题意可得B1(x0,x0),
A1(x0,$\frac{2}{{x}_{0}-1}$),B2($\frac{2}{{x}_{0}-1}$,$\frac{2}{{x}_{0}-1}$),
A2($\frac{2}{{x}_{0}-1}$,$\frac{2}{\frac{2}{{x}_{0}-1}-1}$),
B3($\frac{2}{\frac{2}{{x}_{0}-1}-1}$,$\frac{2}{\frac{2}{{x}_{0}-1}-1}$),
…
即有yn+1=f(yn)=$\frac{2}{{y}_{n}-1}$(yn>1);
(2)由B0($\frac{11}{5}$,0),
可得数列{yn}的所有项为:$\frac{11}{5}$,$\frac{5}{3}$,3,1;
(3)设B0(x0,0),由(1)可得,
令yn+1=yn=t,(t>1),
即有t=$\frac{2}{t-1}$,即为t2-t-2=0,
解得t=2(-1舍去).
则x0为2时,数列{yn}是一个无穷的常数列.
点评 本题数列的递推式的求法,注意运用分析法,考查数列的项的求法,注意运用列举法,同时考查常数列的求法,注意运用方程的思想,考查运算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 1 | B. | -1 | C. | 1996 | D. | -1996 |
