题目内容

10．已知x，y∈R，且满足$\left\{\begin{array}{l}{x≥1}\\{y≥x}\\{x-2y+3≥0}\end{array}\right.$，则$t=\frac{y+1}{x}$的最大值为（　　）
A．3B．2C．1D．$\frac{1}{2}$

分析 作出不等式组对应的平面区域，利用t的几何意义进行求解即可．

解答 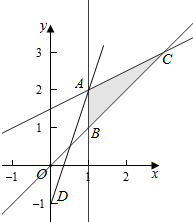解：作出不等式组对应的平面区域如图，$t=\frac{y+1}{x}$的几何意义是区域内的点到点（0，-1）的斜率，
由图象知AD的斜率最大，
由$\left\{\begin{array}{l}{x=1}\\{x-2y+3=0}\end{array}\right.$，得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$，即A（1，2），
则$t=\frac{y+1}{x}$的最大值为t=$\frac{2+1}{1}$=3，
故选：A．

点评 本题主要考查线性规划的应用，根据直线的斜率公式以及数形结合是解决本题的关键．

练习册系列答案
相关题目
20．设F1（-1，0），F2（1，0）是椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点，P为E的上顶点，若$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=2，则a=（　　）
A．1B．2C．$\sqrt{2}$D．4
1．函数$f（x）=sinx-\sqrt{3}cosx，\;x∈[0，\frac{π}{2}]$的值域是[-$\sqrt{3}$，1]．
18．已知实数x，y满足条件$\left\{\begin{array}{l}x-y≥-1\\ x+y≤4\\ x-2y≤0\end{array}\right.$，若使z=ax+y取到最大值的最优解有无数个，则实数a=（　　）
A．-1B．1C．±1D．$-\frac{1}{2}$
5．正三棱柱ABC-A1B1C1中，AB=AA1=a，M是AA1的中点，求面MBC与面ABC所夹的角．
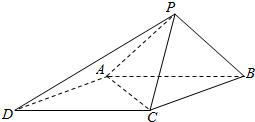15．如图，已知在四陵锥P-ABCD中，底面ABCD是边长为2的菱形，∠BCD=120°，AP=BP，∠APB=90°，PC=2．
（1）求证：AB⊥PC；
（2）求二面角B-PC一D的余弦值．
2．已知函数f（x）=x2+ax+1，
（Ⅰ）设g（x）=（2x-3）f（x），若y=g（x）与x轴恰有两个不同的交点，试求a的取值集合；
（Ⅱ）求函数y=|f（x）|在[0，1]上的最大值．
19．函数f（x）=$\left\{\begin{array}{l}{{3}^{x}-a，x＜1}\\{（x-a）（x-3a），x≥1}\end{array}\right.$，若函数f（x）恰好有两个零点，则实数a的取值范围是$\frac{1}{3}$≤a＜1或a≥3．
20．已知椭圆C：$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1（a＞b＞0）的两个焦点为F1，F2，其离心率为$\frac{1}{2}$，点P是椭圆C上一点，若△PF1F2的面积为1且其内切圆的半径为$\frac{1}{3}$．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若点Q为椭圆C上异于长轴端点A1，A2的动点，定直线y=4与直线QA1、QA2分别相交于M、N两点，已知点G（0，7），试判断y轴上是否存在不同于点G的定点H，使得M，N，G，H四点共圆？若存在，求出点H的坐标；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网