题目内容
19.为了了解某校学生喜欢吃辣是否与性别有关,随机对此校100人进行调查,得到如下的列表:| 喜欢吃辣 | 不喜欢吃辣 | 合计 | |
| 男生 | 40 | 10 | 50 |
| 女生 | 20 | 30 | 50 |
| 合计 | 60 | 40 | 100 |
| p(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)是否有99.9%以上的把握认为喜欢吃辣与性别有关?说明理由.
分析 (1)计算对于的数据,补充出2×2列联表即可;(2)计算k2的值,从而判断结论即可.
解答 解:(1)∵在全部100人中随机抽取1人抽到喜欢吃辣的学生的概率为$\frac{3}{5}$.
∴在100人中,喜欢吃辣的有$\frac{3}{5}×100=60$,∴男生喜欢吃辣的有60-20=40,
列表补充如下:
| 喜欢吃辣 | 不喜欢吃辣 | 合计 | |
| 男生 | 40 | 10 | 50 |
| 女生 | 20 | 30 | 50 |
| 合计 | 60 | 40 | 100 |
(2)∵${K^2}=\frac{{100×{{({40×30-20×10})}^2}}}{50×50×60×40}=\frac{50}{3}≈16.667>10.828$
∴有99.9%以上的把握认为喜欢吃辣与性别有关.…(10分)
点评 本题考查了独立性检验,考查计算能力,是一道基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.下列运算中,正确的是( )
| A. | x3•x2=x5 | B. | x+x2=x3 | C. | 2x3÷x2=x | D. | ($\frac{x}{2}$)3=$\frac{{x}^{3}}{2}$ |
4.从某实验班45名同学中随机抽取5名同学参加“挑战杯”竞赛,用随机数法确定这5名同学,现将随机数表摘录部分如下:
从随机数表第一行的第5列和第6列数字开始由左到右依次选取两个数字,则选出的第5个同学的编号为( )
| 16 | 22 | 77 | 94 | 39 | 49 | 54 | 43 | 54 | 82 | 17 | 37 | 93 | 23 | 78 | 87 | 35 | 20 | 96 | 43 |
| 84 | 42 | 17 | 53 | 31 | 57 | 24 | 55 | 06 | 88 | 77 | 04 | 74 | 47 | 67 | 21 | 76 | 33 | 50 | 25 |
| A. | 23 | B. | 37 | C. | 35 | D. | 17 |
9.在△ABC中,若$|\overrightarrow{AB}|=2$,$|\overrightarrow{AC}|=3$,$|\overrightarrow{BC}|=4$,O为△ABC的内心,且$\overrightarrow{AO}=λ\overrightarrow{AB}+μ\overrightarrow{BC}$,则λ+μ=( )
| A. | $\frac{3}{4}$ | B. | $\frac{5}{9}$ | C. | $\frac{7}{9}$ | D. | $\frac{5}{7}$ |
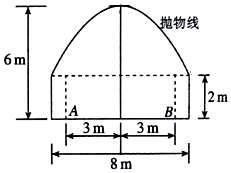 如图所示,一隧道内设双行线公路,其截面由一个长方形和抛物线构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米,已知行车道总宽度|AB|=6米,那么车辆通过隧道的限制高度是多少米?
如图所示,一隧道内设双行线公路,其截面由一个长方形和抛物线构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米,已知行车道总宽度|AB|=6米,那么车辆通过隧道的限制高度是多少米?