题目内容
14.△ABC的三个内角A,B,C的对边分别是a,b,c,$\frac{cosA-2cosC}{cosB}=\frac{2c-a}{b}$.(1)若C=A+$\frac{π}{3}$,求角A的大小;
(2)若cosB=$\frac{1}{4}$,△ABC的周长为5,求b的值.
分析 (1)运用正弦定理和三角形的内角和定理可得角A;
(2)根据余弦定理求出a,b,c的关系,根据,△ABC的周长为5,即可求b的值.
解答 解:由$\frac{cosA-2cosC}{cosB}=\frac{2c-a}{b}$.
可得:$\frac{cosA-2cosC}{cosB}=\frac{2sinC-sinA}{sinB}$
?cosAsinB-2sinBcosC=2cosBsinC-sinAcosB
?cosAsinB+sinAcosB=2cosBsinC+2sinBcosC
?sin(A+B)=2sin(B+C)
?sinC=2sinA,即c=2a
(1)∵C=A+$\frac{π}{3}$,
∴sin(A+$\frac{π}{3}$)=2sinA
可得:$\frac{1}{2}$sinA+$\frac{\sqrt{3}}{2}$cosA=2sinA
$\sqrt{3}$sin(A-$\frac{π}{6}$)=0,
∵△ABC的三个内角A,B,C.
∴A=$\frac{π}{6}$.
(2)cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{1}{4}$,△ABC的周长为5=a+b+c
∵c=2a
∴$\left\{\begin{array}{l}{5=b+3a}\\{4{a}^{2}-{b}^{2}=0}\end{array}\right.$,解得:b=2.
故b的值为2.
点评 本题考查三角形的正余弦定理和内角和定理的运用,考查运算能力,属于基础题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
9.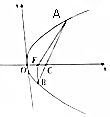 如图,设抛物线y2=4x的焦点为F,不经过焦点的直线上有三个不同的点A,B,C,其中点A,B在抛物线上,点C在x轴上,记△BCF的面积为S1,△ACF的面积为S2,则$\frac{{S}_{1}^{2}}{{S}_{2}^{2}}$等于是( )
如图,设抛物线y2=4x的焦点为F,不经过焦点的直线上有三个不同的点A,B,C,其中点A,B在抛物线上,点C在x轴上,记△BCF的面积为S1,△ACF的面积为S2,则$\frac{{S}_{1}^{2}}{{S}_{2}^{2}}$等于是( )
 如图,设抛物线y2=4x的焦点为F,不经过焦点的直线上有三个不同的点A,B,C,其中点A,B在抛物线上,点C在x轴上,记△BCF的面积为S1,△ACF的面积为S2,则$\frac{{S}_{1}^{2}}{{S}_{2}^{2}}$等于是( )
如图,设抛物线y2=4x的焦点为F,不经过焦点的直线上有三个不同的点A,B,C,其中点A,B在抛物线上,点C在x轴上,记△BCF的面积为S1,△ACF的面积为S2,则$\frac{{S}_{1}^{2}}{{S}_{2}^{2}}$等于是( )| A. | $\frac{{|{BF}|-1}}{{|{AF}|-1}}$ | B. | $\frac{{{{|{BF}|}^2}-1}}{{{{|{AF}|}^2}-1}}$ | C. | $\frac{{|{BF}|+1}}{{|{AF}|+1}}$ | D. | $\frac{{{{|{BF}|}^2}+1}}{{{{|{AF}|}^2}+1}}$ |
19.为了了解某校学生喜欢吃辣是否与性别有关,随机对此校100人进行调查,得到如下的列表:
已知在全部100人中随机抽取1人抽到喜欢吃辣的学生的概率为$\frac{3}{5}$.
(1)请将上面的列表补充完整;
(2)是否有99.9%以上的把握认为喜欢吃辣与性别有关?说明理由.
| 喜欢吃辣 | 不喜欢吃辣 | 合计 | |
| 男生 | 40 | 10 | 50 |
| 女生 | 20 | 30 | 50 |
| 合计 | 60 | 40 | 100 |
| p(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)是否有99.9%以上的把握认为喜欢吃辣与性别有关?说明理由.
6.已知实数a满足下列两个条件:
①关于x的方程ax2+3x+1=0有解;
②代数式log2(a+3)有意义.
则使得指数函数y=(3a-2)x为减函数的概率为( )
①关于x的方程ax2+3x+1=0有解;
②代数式log2(a+3)有意义.
则使得指数函数y=(3a-2)x为减函数的概率为( )
| A. | $\frac{4}{63}$ | B. | $\frac{1}{16}$ | C. | $\frac{3}{63}$ | D. | $\frac{3}{16}$ |
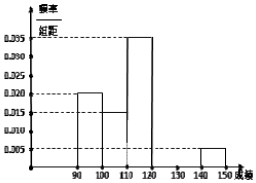 某校高三数学竞赛初赛考试结束后,对考生成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分为六组,第一组.如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
某校高三数学竞赛初赛考试结束后,对考生成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分为六组,第一组.如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.