题目内容
数列{an}的前n项和Sn满足Sn=
,则a6= .
| 2n |
| n+1 |
考点:数列的概念及简单表示法
专题:点列、递归数列与数学归纳法
分析:根据题中给出的数列{an}的前n项和的公式便可求出数列{an}的通项公式,将n=6代入通项公式便可得出答案.
解答:
解:S6-S5=
-
=
,
所以a6=
;
故答案为:
.
| 2×6 |
| 6+1 |
| 2×5 |
| 5+1 |
| 1 |
| 21 |
所以a6=
| 1 |
| 21 |
故答案为:
| 1 |
| 21 |
点评:本题考查了数列的基本知识,考查了学生的计算能力,解题时要认真审题,仔细解答,避免错误,属于中档题.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
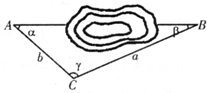 如图,为了测量隧道两口之间AB的长度,对给出的四组数据,求解计算时,较为简便易行的一组是( )
如图,为了测量隧道两口之间AB的长度,对给出的四组数据,求解计算时,较为简便易行的一组是( )| A、a,b,γ |
| B、a,b,α |
| C、a,b,β |
| D、α,β,a |
已知坐标原点O在圆x2+y2-x+y+m=0外,则m的取值范围是( )
A、0<m<
| ||
B、m<
| ||
C、m≤
| ||
| D、m>0 |
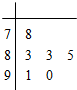 对某同学的6次数学测试成绩(满分100分)进行统计,作出的茎叶图如图所示,给出关于该同学数学成绩的以下说法:
对某同学的6次数学测试成绩(满分100分)进行统计,作出的茎叶图如图所示,给出关于该同学数学成绩的以下说法:①中位数为84;
②众数为85;
③平均数为85;
④极差为12.
其中,正确说法的序号是( )
| A、①② | B、③④ | C、②④ | D、①③ |
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的部分图象如图示,则下列说法不正确的是( )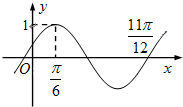
| π |
| 2 |

| A、ω=2 | ||||
B、f(x)的图象关于点(
| ||||
C、k(x)=f(
| ||||
| D、已知函数g(x)=cos(ξx+η)图象与f(x)的对称轴完全相同,则ξ=2 |
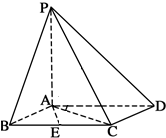 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点.