题目内容
12. 如图,在长方体ABCD-A1B1C1D1中,$AB=\sqrt{3}AD=\sqrt{3}A{A_1}=\sqrt{3}$,点P为线段A1C上的动点(包含线段端点),则下列结论正确的①②.
如图,在长方体ABCD-A1B1C1D1中,$AB=\sqrt{3}AD=\sqrt{3}A{A_1}=\sqrt{3}$,点P为线段A1C上的动点(包含线段端点),则下列结论正确的①②.①当$\overrightarrow{{A_1}C}=3\overrightarrow{{A_1}P}$时,D1P∥平面BDC1;
②当$\overrightarrow{{A_1}C}=5\overrightarrow{{A_1}P}$时,A1C⊥平面D1AP;
③当∠APD1的最大值为90°;
④AP+PD1的最小值为$\sqrt{5}$.
分析 以D为原点建立空间直角坐标系,设AA1=1,则AD=1,AB=$\sqrt{3}$,设$\overrightarrow{{A}_{1}C}=λ\overrightarrow{{A}_{1}P}$;(λ≥1)
则A(1,0,0),C(0,$\sqrt{3}$,0),A1(1,0,1),D1(0,0,1),C1(0,$\sqrt{3}$,1),B(1,$\sqrt{3}$,0),$\overrightarrow{{A}_{1}C}=(-1,\sqrt{3},-1)$,$\overrightarrow{{A}_{1}P}=\frac{1}{λ}\overrightarrow{{A}_{1}C}=(-\frac{1}{λ},\frac{\sqrt{3}}{λ},-\frac{1}{λ})$,$\overrightarrow{{D}_{1}A}=(1,0,-1)$
利用向量与位置关系的等价性逐一判定即可,
解答 解:如图,以D为原点建立空间直角坐标系,设AA1=1,则AD=1,AB=$\sqrt{3}$,设$\overrightarrow{{A}_{1}C}=λ\overrightarrow{{A}_{1}P}$;(λ≥1)
则A(1,0,0),C(0,$\sqrt{3}$,0),A1(1,0,1),D1(0,0,1),C1(0,$\sqrt{3}$,1),B(1,$\sqrt{3}$,0)
$\overrightarrow{{A}_{1}C}=(-1,\sqrt{3},-1)$,$\overrightarrow{{A}_{1}P}=\frac{1}{λ}\overrightarrow{{A}_{1}C}=(-\frac{1}{λ},\frac{\sqrt{3}}{λ},-\frac{1}{λ})$,$\overrightarrow{{D}_{1}A}=(1,0,-1)$
对于①,设平面DBC1的法向量为$\overrightarrow{n}=(x,y,z)$
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{D{C}_{1}}=\sqrt{3}y+z=0}\\{\overrightarrow{n}•\overrightarrow{DB}=x+\sqrt{3}y=0}\end{array}\right.$可得$\overrightarrow{n}=(-\sqrt{3},1,-\sqrt{3})$
$\overrightarrow{{D}_{1}P}=(1-\frac{1}{λ},\frac{\sqrt{3}}{λ},-\frac{1}{λ})$
若D1P∥平面BDC1,则$\overrightarrow{{D}_{1}P}•\overrightarrow{n}=0$,解得λ=3,故①正确.
对于②,若A1C⊥平面D1AP,则$\left\{\begin{array}{l}{\overrightarrow{{A}_{1}C}•\overrightarrow{{D}_{1}P}=0}\\{\overrightarrow{{A}_{1}C}•\overrightarrow{{D}_{1}A}=0}\end{array}\right.$,解得λ=5,故②正确;
对于③,$\overrightarrow{P{D}_{1}}•\overrightarrow{PA}=\frac{4}{{λ}^{2}}-\frac{2}{λ}$<0 (λ≥1)有解,故∠APD1可以大于900.所以③错;
对于④,∵$\overrightarrow{P{D}_{1}}•\overrightarrow{PA}=\frac{4}{{λ}^{2}}-\frac{2}{λ}$=0时,λ=2,此时AP+PD1=$\sqrt{5}$,
当λ>2时,∠APD1为钝角此时AP+PD1小于$\sqrt{5}$,故④错
综上,故答案为:①②.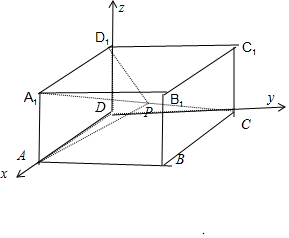
点评 本题考查了空间线面、线线的位置关系,及动点问题的处理,借助向量进行运算处理动点问题是常见的技巧,属于中档题.

 中考解读考点精练系列答案
中考解读考点精练系列答案| A. | {x|3≤x<7}, | B. | {x|2<x<10} | C. | {x|x≤2或x≥10} | D. | {x|x<3或x≥7} |
产品A产品B(其中p、q>0)
| 投资结果 | 获利40% | 不赔不赚 | 亏损20% |
| 概 率 | $\frac{1}{3}$ | $\frac{1}{2}$ | $\frac{1}{6}$ |
| 投资结果 | 获利20% | 不赔不赚 | 亏损10% |
| 概 率 | p | $\frac{1}{3}$ |
(Ⅱ)丙要将家中闲置的10万元钱进行投资,以一年后投资收益的期望值为决策依据,在产品A和产品B之中选其一,应选用哪个?
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | $1+\frac{{\sqrt{2}}}{2}$ | B. | 1 | C. | $1-\frac{{\sqrt{2}}}{2}$ | D. | 0 |
 如图,在直三棱柱ABC-A1B1C1中,△ABC是正三角形,E是棱BB1的中点.
如图,在直三棱柱ABC-A1B1C1中,△ABC是正三角形,E是棱BB1的中点.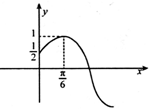 已知函数$f(x)=Asin({ωx+φ})({A>0,ω>0,0<φ<\frac{π}{2}})$的部分图象如图所示,将f(x)的图象向右平移$\frac{π}{6}$个单位得到函数g(x)的图象.
已知函数$f(x)=Asin({ωx+φ})({A>0,ω>0,0<φ<\frac{π}{2}})$的部分图象如图所示,将f(x)的图象向右平移$\frac{π}{6}$个单位得到函数g(x)的图象.