题目内容
7. 如图,在直三棱柱ABC-A1B1C1中,△ABC是正三角形,E是棱BB1的中点.
如图,在直三棱柱ABC-A1B1C1中,△ABC是正三角形,E是棱BB1的中点.(Ⅰ)求证:平面AEC1⊥平面AA1C1C;
(Ⅱ)若AA1=AB=1,求点E到平面ABC1的距离.
分析 (I)分别取AC,AC1的中点O,F,连接OB,OF,EF,则$OF\underset{∥}{=}BE$,可得四边形OBEF为平行四边形,可得:OB∥EF.由已知可得:OB⊥平面ACC1A1,即可证明EF⊥平面ACC1A1,∴平面AEC1⊥平面AA1C1C.
(II)设点E到平面ABC1的距离为h1.点C1到平面ABE的距离为h2.利用${V}_{E-AB{C}_{1}}$=$\frac{1}{3}×{S}_{△AB{C}_{1}}$×h1=${V}_{{C}_{1}-ABE}$═$\frac{1}{3}×{S}_{△ABE}$×h2,即可得出.
解答 (I)证明:分别取AC,AC1的中点O,F,连接OB,OF,EF,则$OF\underset{∥}{=}BE$,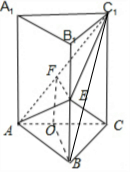
∴四边形OBEF为平行四边形,可得:OB∥EF.∵直三棱柱ABC-A1B1C1中,
△ABC是正三角形,O是AC的中点,∴OB⊥平面ACC1A1,∴EF⊥平面ACC1A1,
∴平面AEC1⊥平面AA1C1C.
(II)解:设点E到平面ABC1的距离为h1.点C1到平面ABE的距离为h2.
∴${V}_{E-AB{C}_{1}}$=$\frac{1}{3}×{S}_{△AB{C}_{1}}$×h1=${V}_{{C}_{1}-ABE}$=$\frac{1}{3}×{S}_{△ABE}$×h2=$\frac{1}{3}×\frac{1}{4}×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{24}$.
又BC1=AC1=$\sqrt{2}$,AB=1.
∴${S}_{△AB{C}_{1}}$=$\frac{\sqrt{7}}{4}$,∴h1=$\frac{\sqrt{21}}{14}$.
∴点E到平面ABC1的距离为$\frac{\sqrt{21}}{14}$.
点评 本题考查了空间位置关系、等边三角形的判定与性质、三棱锥的体积计算公式、空间距离,考查了推理能力与计算能力,属于中档题.

| A. | p∨q | B. | p∧q | C. | ¬p∧q | D. | ¬p∨q |
| A. | {x|0<x<2} | B. | {x|-1<x<3} | C. | {x|-1<x<0} | D. | {x|2<x<3} |
| A. | $[{-\frac{3}{4},0}]$ | B. | $[{0,\frac{3}{4}}]$ | C. | $({-\frac{3}{4},0})$ | D. | $({0,\frac{3}{4}})$ |
 如图,在长方体ABCD-A1B1C1D1中,$AB=\sqrt{3}AD=\sqrt{3}A{A_1}=\sqrt{3}$,点P为线段A1C上的动点(包含线段端点),则下列结论正确的①②.
如图,在长方体ABCD-A1B1C1D1中,$AB=\sqrt{3}AD=\sqrt{3}A{A_1}=\sqrt{3}$,点P为线段A1C上的动点(包含线段端点),则下列结论正确的①②.