题目内容
6.已知|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=8,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为150°.计算:(1)($\overrightarrow{a}$$+2\overrightarrow{b}$)•(2$\overrightarrow{a}$-$\overrightarrow{b}$);
(2)|4$\overrightarrow{a}$-2$\overrightarrow{b}$|
分析 (1)直接利用向量的数量积的运算法则化简求解即可.
(2)利用向量的模的求法否则化简求解即可.
解答 解:(1)|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=8,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为150°.
($\overrightarrow{a}$$+2\overrightarrow{b}$)•(2$\overrightarrow{a}$-$\overrightarrow{b}$)=2${\overrightarrow{a}}^{2}$+3$\overrightarrow{a}•\overrightarrow{b}$-2${\overrightarrow{b}}^{2}$=2×16+3×$4×8×(-\frac{\sqrt{3}}{2})$-2×64=-96-48$\sqrt{3}$;
(2)|4$\overrightarrow{a}$-2$\overrightarrow{b}$|=$\sqrt{16{\overrightarrow{a}}^{2}-16\overrightarrow{a}•\overrightarrow{b}+4{\overrightarrow{b}}^{2}}$=$\sqrt{16×16+16×4×8×\frac{\sqrt{3}}{2}+4×64}$=8$\sqrt{8+4\sqrt{3}}$=16$\sqrt{2+\sqrt{3}}$.
点评 本题考查平面向量的数量积的运算,向量的模的求法,考查计算能力.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
18.下列说法正确的是( )
| A. | 函数y=2x2-x+1在(0,+∞)上是增函数 | |
| B. | 幂函数在(0,+∞)上都是增函数 | |
| C. | 函数y=log2(x+$\sqrt{{x}^{2}+1}$)既不是奇函数,也不是偶函数 | |
| D. | 已知f(x)是定义在R上的增函数,若a+b>0,则有f(a)+f(b)>f(-a)+f(-b) |
17.对于曲线C所在平面内的点O,若存在以O为顶点的角θ,使得θ≥∠AOB对于曲线C上的任意两个不同点A、B恒成立,则称θ为曲线C相对于O的“界角”,并称最小的“界角”为曲线C相对于O的“确界角”,已知曲线M:y=$\left\{\begin{array}{l}{\sqrt{1+9{x}^{2}},x≤0}\\{1+x{e}^{x-1},x>0}\end{array}\right.$,(其中e为自然对数的底数),O为坐标原点,则曲线M相对于O的“确界角”为( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{2π}{3}$ | D. | $\frac{3π}{4}$ |
18.计算:cos24°cos36°-cos66°cos54°=( )
| A. | 0 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
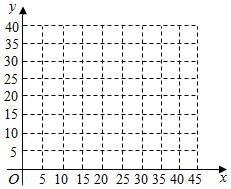 某公司为员工采购两年年终奖品,要求平板电脑的数量至多比手机多5部,预算经费12万,已知手机4千元一部,平板3千元一部,采购的手机和平板电脑的数量分别为x,y
某公司为员工采购两年年终奖品,要求平板电脑的数量至多比手机多5部,预算经费12万,已知手机4千元一部,平板3千元一部,采购的手机和平板电脑的数量分别为x,y