题目内容
15.已知直线ax+y-1=0与圆x2+y2-2x-8y+13=0交于A,B两点.若|AB|=2$\sqrt{3}$,则实数a的值是( )| A. | -$\frac{4}{3}$ | B. | -$\frac{3}{4}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 圆方程化为标准方程,找出圆心坐标与半径r,利用点到直线的距离公式表示出圆心到已知直线的距离d,根据弦长,利用垂径定理及勾股定理列出关于a的方程,求出方程的解即可得到a的值.
解答 解:圆方程化为(x-1)2+(y-4)2=4,可得圆心(1,4),半径r=2,
∵弦长|AB|=2$\sqrt{3}$,圆心到直线的距离d=$\sqrt{4-3}$=$\frac{|a+3|}{\sqrt{{a}^{2}+1}}$,
解得:a=-$\frac{4}{3}$,
故选A.
点评 此题考查了直线与圆相交的性质,涉及的知识有:圆的标准方程,点到直线的距离公式,垂径定理,勾股定理,熟练掌握公式及定理是解本题的关键.

练习册系列答案
相关题目
5.在△OMN中,点A在OM上,点B在ON上,且AB∥MN,2OA=OM,若$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则终点P落在四边形ABNM内(含边界)时,$\frac{y+x+2}{x+1}$的取值范围是( )
| A. | $[\frac{1}{2},2]$ | B. | $[\frac{1}{3},3]$ | C. | $[\frac{3}{2},3]$ | D. | $[\frac{4}{3},4]$ |
10.为了研究某学科成绩是否与学生性别有关,采用分层抽样的方法,从高二年级抽取了30名男生和20名女生的该学科成绩,得到如图所示男生成绩的频率分布直方图和女生成绩的茎叶图,规定80分以上为优分(含80分).
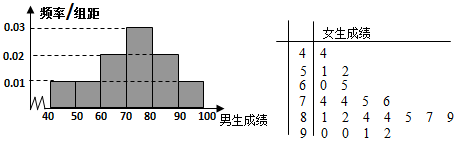
(Ⅰ)(i)请根据图示,将2×2列联表补充完整;
(ii)据列联表判断,能否在犯错误概率不超过10%的前提下认为“学科成绩与性别有关”?
(Ⅱ)将频率视作概率,从高二年级该学科成绩中任意抽取3名学生的成绩,求成绩为优分人数X的分布列与数学期望.
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$(n=a+b+c+d).
参考数据:

(Ⅰ)(i)请根据图示,将2×2列联表补充完整;
| 优分 | 非优分 | 总计 | |
| 男生 | |||
| 女生 | |||
| 总计 | 50 |
(Ⅱ)将频率视作概率,从高二年级该学科成绩中任意抽取3名学生的成绩,求成绩为优分人数X的分布列与数学期望.
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$(n=a+b+c+d).
参考数据:
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
7.tan$\frac{π}{4}$等于( )
| A. | -1 | B. | 1 | C. | -$\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
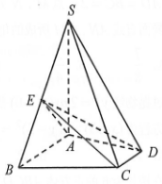 如图,已知四棱锥S-ABCD中,SA⊥平面ABCD,∠ABC=∠BCD=90°,且SA=AB=BC=2CD=2,E是边SB的中点.
如图,已知四棱锥S-ABCD中,SA⊥平面ABCD,∠ABC=∠BCD=90°,且SA=AB=BC=2CD=2,E是边SB的中点.