题目内容
5.若f(x)=ax2+(a-2)x+a2是偶函数,则${∫}_{-a}^{a}$(x2+x+$\sqrt{4-{x}^{2}}$)dx=$\frac{28}{3}$+2π.分析 根据函数的奇偶性求出a的值,求定积分的值即可.
解答 解:若f(x)=ax2+(a-2)x+a2是偶函数,
则a-2=0,即a=2,
故f(x)=2x2+4,
则${∫}_{-a}^{a}$(x2+x+$\sqrt{4-{x}^{2}}$)dx=${∫}_{-2}^{2}$x2dx+${∫}_{-2}^{2}$xdx+${∫}_{-2}^{2}$$\sqrt{4{-x}^{2}}$dx
=$\frac{1}{3}$x3${|}_{-2}^{2}$+$\frac{1}{2}$x2${|}_{-2}^{2}$+2π
=$\frac{28}{3}$+2π,
故答案为:$\frac{28}{3}$+2π.
点评 本题考查了函数的奇偶性问题,考查求定积分的值,是一道中档题.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
15.已知直线ax+y-1=0与圆x2+y2-2x-8y+13=0交于A,B两点.若|AB|=2$\sqrt{3}$,则实数a的值是( )
| A. | -$\frac{4}{3}$ | B. | -$\frac{3}{4}$ | C. | $\sqrt{3}$ | D. | 2 |
16.在直角坐标平面内,点A,B的坐标分别为(-1,0),(1,0),则满足tan∠PAB•tan∠PBA=m(m为非零常数)的点P的轨迹方程是( )
| A. | ${x^2}-\frac{y^2}{m}=1(y≠0)$ | B. | ${x^2}-\frac{y^2}{m}=1$ | C. | ${x^2}+\frac{y^2}{m}=1(y≠0)$ | D. | ${x^2}+\frac{y^2}{m}=1$ |
13.若a<b,d<c,并且(c-a)(c-b)<0,(d-a)(d-b)>0,则a、b、c、d的大小关系是( )
| A. | d<a<c<b | B. | a<c<b<d | C. | a<d<b<c | D. | a<d<c<b |
20.若等比数列{an}的前n项和Sn=3n+1+a,则a=( )
| A. | 1 | B. | -1 | C. | 3 | D. | -3 |
4.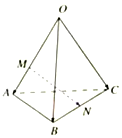 如图,空间四边形OABC中,点M、N分别OA、BC上,OM=2MA、BN=CN,则$\overrightarrow{MN}$=( )
如图,空间四边形OABC中,点M、N分别OA、BC上,OM=2MA、BN=CN,则$\overrightarrow{MN}$=( )
 如图,空间四边形OABC中,点M、N分别OA、BC上,OM=2MA、BN=CN,则$\overrightarrow{MN}$=( )
如图,空间四边形OABC中,点M、N分别OA、BC上,OM=2MA、BN=CN,则$\overrightarrow{MN}$=( )| A. | $\frac{1}{2}\overrightarrow{OA}-\frac{2}{3}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$ | B. | $-\frac{2}{3}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$ | C. | $\frac{1}{2}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OC}$ | D. | $\frac{2}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OC}$ |