题目内容
5.在△OMN中,点A在OM上,点B在ON上,且AB∥MN,2OA=OM,若$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则终点P落在四边形ABNM内(含边界)时,$\frac{y+x+2}{x+1}$的取值范围是( )| A. | $[\frac{1}{2},2]$ | B. | $[\frac{1}{3},3]$ | C. | $[\frac{3}{2},3]$ | D. | $[\frac{4}{3},4]$ |
分析 利用向量知识可知,推出点Q(x,y)落 在平面直角坐标系中两直线x+y=1,x+y=2及x轴、y轴围成的四边形(含边界)内.画出图形,利用目标函数的几何意义求解即可.
解答 解:由题意,点P(x,y)落 在平面直角坐标系中两直线x+y=1,x+y=2及x轴、y轴围成的四边形(含边界)内.又因为$\frac{y+x+2}{x+1}=\frac{y+1}{x+1}+1=k+1$,其中$k=\frac{y+1}{x+1}$表示点Q(-1,-1)与点P连线的斜率.
由图形可知$\frac{1}{3}≤k≤3$,所以$\frac{4}{3}≤\frac{y+x+2}{x+1}≤4$.
故选:D.
点评 本题主要考查线性规划的应用,利用z的几何意义,通过数形结合是解决本题的关键.

练习册系列答案
相关题目
15.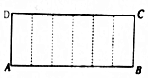 已知矩形ABCD的周长为18,把它沿图中的虚线折成正六棱柱,当这个正六棱柱的体积最大时,它的外接球的表面积为( )
已知矩形ABCD的周长为18,把它沿图中的虚线折成正六棱柱,当这个正六棱柱的体积最大时,它的外接球的表面积为( )
 已知矩形ABCD的周长为18,把它沿图中的虚线折成正六棱柱,当这个正六棱柱的体积最大时,它的外接球的表面积为( )
已知矩形ABCD的周长为18,把它沿图中的虚线折成正六棱柱,当这个正六棱柱的体积最大时,它的外接球的表面积为( )| A. | 13π | B. | 12π | C. | 11π | D. | 10π |
16.已知函数f(x)=lgx,0<a<b,若p=f($\sqrt{ab}$),q=f($\frac{a+b}{2}$),r=$\frac{1}{2}$[f(a)+f(b)],则p,q,r的大小关系是( )
| A. | p=r>q | B. | p=r<q | C. | q=r<p | D. | q-r>p |
20.“一条直线l与平面α内无数条直线异面”是“这条直线与平面α平行”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
17.函数$y={log_a}({2{x^2}-3x+1})$,当x=3时,y<0则该函数的单调递减区间是( )
| A. | $({-∞,\frac{3}{4}})$ | B. | $({\frac{3}{4},+∞})$ | C. | $({-∞,\frac{1}{2}})$ | D. | (1,+∞) |
14.某青年教师有一专项课题是进行“学生数学成绩与物理成绩的关系”的研究,他调查了某中学高二年级800名学生上学期期末考试的数学和物理成绩,把成绩按优秀和不优秀分类得到的结果是:数学和物理都优秀的有60人,数学成绩优秀但物理不优秀的有140人,物理成绩优秀但数学不优秀的有60人.
(1)能否在犯错概率不超过0.001的前提下认为该中学学生的数学成绩与物理成绩有关?
(2)将上述调查所得到的频率视为概率,从全体高二年级学生成绩中,有放回地随机抽取4名学生的成绩,记抽取的4份成绩中数学、物理两科成绩恰有一科优秀的份数为X,求X的分布列和期望E(X).
附:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
(1)能否在犯错概率不超过0.001的前提下认为该中学学生的数学成绩与物理成绩有关?
(2)将上述调查所得到的频率视为概率,从全体高二年级学生成绩中,有放回地随机抽取4名学生的成绩,记抽取的4份成绩中数学、物理两科成绩恰有一科优秀的份数为X,求X的分布列和期望E(X).
附:
| P(K2≥k0) | 0.100 | 0.050 | 0.010 |
| k0 | 6.635 | 7.879 | 10.828 |
15.已知直线ax+y-1=0与圆x2+y2-2x-8y+13=0交于A,B两点.若|AB|=2$\sqrt{3}$,则实数a的值是( )
| A. | -$\frac{4}{3}$ | B. | -$\frac{3}{4}$ | C. | $\sqrt{3}$ | D. | 2 |