题目内容
20.已知向量$\overrightarrow{a}$=(1,0,-1),$\overrightarrow{b}$=(-1,-1,0),则|$\overrightarrow{a}$|的值是$\sqrt{2}$,向量$\overrightarrow{a}$与$\overrightarrow{b}$之间的夹角是120°.分析 由已知向量的坐标利用向量模的公式求$|\overrightarrow{a}|、|\overrightarrow{b}|$,进一步求得$\overrightarrow{a}•\overrightarrow{b}$,代入数量积求夹角公式求得向量$\overrightarrow{a}$与$\overrightarrow{b}$之间的夹角.
解答 解:由$\overrightarrow{a}$=(1,0,-1),$\overrightarrow{b}$=(-1,-1,0),
得$|\overrightarrow{a}|=\sqrt{{1}^{2}+{0}^{2}+(-1)^{2}}=\sqrt{2}$,
$|\overrightarrow{b}|=\sqrt{(-1)^{2}+(-1)^{2}+{0}^{2}}=\sqrt{2}$,
$\overrightarrow{a}•\overrightarrow{b}=-1$,
∴cos<$\overrightarrow{a},\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}=-\frac{1}{2}$,
∴向量$\overrightarrow{a}$与$\overrightarrow{b}$之间的夹角是120°.
故答案为:$\sqrt{2},{120°}$.
点评 本题考查数量积表示向量的夹角,考查向量模的求法,是基础的计算题.

练习册系列答案
相关题目
11.下列判断错误的是( )
| A. | 命题“若am2≤bm2,则a≤b”是假命题 | |
| B. | 直线y=$\frac{1}{2}$x+b不能作为函数f(x)=$\frac{1}{{e}^{x}}$图象的切线 | |
| C. | “若a=1,则直线x+y=0和直线x-ay=0互相垂直”的逆否命题为真命题 | |
| D. | “f′(x0)=0”是“函数f(x)在x0处取得极值”的充分不必要条件 |
8.某网站对“爱飞客”飞行大会的日关注量x(万人)与日点赞量y(万次)进行了统计对比,得到表格如下:
由散点图象知,可以用回归直线方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$来近似刻画它们之间的关系.
(Ⅰ)求出y关于x的回归直线方程,并预测日关注量为10万人时的日点赞量;
(Ⅱ)一个三口之家参加“爱飞客”亲子游戏,游戏规定:三人依次从装有3个白球和2个红球的箱子中不放回地各摸出一个球,大人摸出每个红球得奖金10元,小孩摸出1个红球得奖金50元.求该三口之家所得奖金总额不低于50元的概率.
参考公式:b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$; 参考数据:$\sum_{i=1}^{5}$xi2=200,$\sum_{i=1}^{5}$xiyi=112.
| x | 3 | 5 | 6 | 7 | 9 |
| y | 2 | 3 | 3 | 4 | 5 |
(Ⅰ)求出y关于x的回归直线方程,并预测日关注量为10万人时的日点赞量;
(Ⅱ)一个三口之家参加“爱飞客”亲子游戏,游戏规定:三人依次从装有3个白球和2个红球的箱子中不放回地各摸出一个球,大人摸出每个红球得奖金10元,小孩摸出1个红球得奖金50元.求该三口之家所得奖金总额不低于50元的概率.
参考公式:b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$; 参考数据:$\sum_{i=1}^{5}$xi2=200,$\sum_{i=1}^{5}$xiyi=112.
15.已知直线ax+y-1=0与圆x2+y2-2x-8y+13=0交于A,B两点.若|AB|=2$\sqrt{3}$,则实数a的值是( )
| A. | -$\frac{4}{3}$ | B. | -$\frac{3}{4}$ | C. | $\sqrt{3}$ | D. | 2 |
12.定义在R上的奇函数f(x)满足在(-∞,0)上为增函数且f(-1)=0,则不等式x•f(x)>0的解集为( )
| A. | (-∞,-1)∪(1,+∞) | B. | (-1,0)∪(0,1) | C. | (-1,0)∪(1,+∞) | D. | (-∞,-1)∪(0,1) |
4.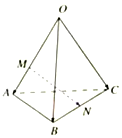 如图,空间四边形OABC中,点M、N分别OA、BC上,OM=2MA、BN=CN,则$\overrightarrow{MN}$=( )
如图,空间四边形OABC中,点M、N分别OA、BC上,OM=2MA、BN=CN,则$\overrightarrow{MN}$=( )
 如图,空间四边形OABC中,点M、N分别OA、BC上,OM=2MA、BN=CN,则$\overrightarrow{MN}$=( )
如图,空间四边形OABC中,点M、N分别OA、BC上,OM=2MA、BN=CN,则$\overrightarrow{MN}$=( )| A. | $\frac{1}{2}\overrightarrow{OA}-\frac{2}{3}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$ | B. | $-\frac{2}{3}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$ | C. | $\frac{1}{2}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OC}$ | D. | $\frac{2}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OC}$ |
 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E,G分别是PA,PB,BC的中点;
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E,G分别是PA,PB,BC的中点;