题目内容
已知sinα=
,sin(α-β)=-
,(0≤α≤
,0≤β≤
),求sinβ的值.
| 3 |
| 5 |
| 4 |
| 5 |
| π |
| 2 |
| π |
| 2 |
考点:两角和与差的正弦函数
专题:三角函数的求值
分析:先利用平方关系分别求得cosα和cos(α-β)的值,进而利用正弦的两角和公式对求得sinβ的值.
解答:
解:∵0≤α≤
,0≤β≤
,
∴-
≤α-β≤
又sin(α-β)=-
,sinα=
,
∴cos(α-β)=
,cosα=
,
∴sinβ=sin[α-(α-β)]=sinαcos(α-β)-cosαsin(α-β)=
×
-
×(-
)=1.
| π |
| 2 |
| π |
| 2 |
∴-
| π |
| 2 |
| π |
| 2 |
又sin(α-β)=-
| 4 |
| 5 |
| 3 |
| 5 |
∴cos(α-β)=
| 3 |
| 5 |
| 4 |
| 5 |
∴sinβ=sin[α-(α-β)]=sinαcos(α-β)-cosαsin(α-β)=
| 3 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
点评:本题主要考查了两角和与差的正弦函数公式的运用.注意对三角函数符号的正确判定.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
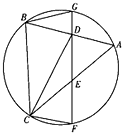 如图,D,E分别是△ABC的边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,BG=BD.
如图,D,E分别是△ABC的边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,BG=BD. 如图甲,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD,E、F、G分别是PC、PD、BC的中点,现将△PDC沿CD折起,使平面PDC⊥平面ABCD(如图乙),且所得到的四棱锥P-ABCD的正视图、侧视图、俯视图的面积总和为8.
如图甲,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD,E、F、G分别是PC、PD、BC的中点,现将△PDC沿CD折起,使平面PDC⊥平面ABCD(如图乙),且所得到的四棱锥P-ABCD的正视图、侧视图、俯视图的面积总和为8.