题目内容
(1)化简:
.
(2)已知sin(π+α)=
,求sin(2π-α)-cot(α-π)•cosα的值.
| sin2(α+π)•cos(π+α)•cot(-α-2π) |
| tan(π+α)•cos3(-α-π) |
(2)已知sin(π+α)=
| 1 |
| 2 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:(1)直接利用诱导公式化简表达式,求出结果即可.
(2)利用诱导公式化简条件,然后化简所求表达式,代入求解即可.
(2)利用诱导公式化简条件,然后化简所求表达式,代入求解即可.
解答:
解:(1)原式=
=
=
=-1
(2)利用诱导公式化简sin(π+α)=
,可得:sinα=-
,
sin(2π-α)-cot(α-π)•cosα
=-sinα-cotα•cosα
=-
-
=-
=2.
| (-sinα)2•(-cosα)•[-cot(2π+α)] |
| tanα•cos3(π+α) |
| sin2α•(-cosα)•cotα |
| tanα•(-cosα)3 |
| sin2α•cosα•cotα |
| -tanα•cos3α |
(2)利用诱导公式化简sin(π+α)=
| 1 |
| 2 |
| 1 |
| 2 |
sin(2π-α)-cot(α-π)•cosα
=-sinα-cotα•cosα
=-
| sin2α |
| sinα |
| cos2α |
| sinα |
| 1 |
| sinα |
点评:本题考查诱导公式化简求解三角函数的值的知识,考查计算能力.

练习册系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积是( )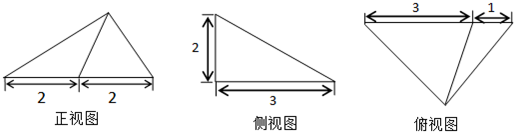

A、
| ||
| B、4 | ||
| C、2 | ||
D、
|
设A与B是相互独立事件,则下列命题正确的是( )
| A、A与B是互斥事件 | ||||
| B、A与B是对立事件 | ||||
C、
| ||||
D、
|
