题目内容
某几何体的三视图如图所示，则该几何体的体积是（ ）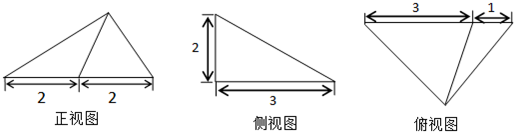
A、
| ||
| B、4 | ||
| C、2 | ||
D、
|
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：由三视图知几何体为三棱锥，且三棱锥的一个侧面与底面垂直，高为2，底面三角形的底边长为4，高为3，把数据代入棱锥的体积公式计算．
解答：
解：由三视图知几何体为三棱锥，且三棱锥的一个侧面与底面垂直，高为2，
底面三角形的底边长为4，高为3，
∴几何体的体积V=
×
×4×3×2=4．
故选：B．
底面三角形的底边长为4，高为3，
∴几何体的体积V=
| 1 |
| 3 |
| 1 |
| 2 |
故选：B．
点评：本题考查了由三视图求几何体的体积，解题的关键是由三视图判断几何体的形状及数据所对应的几何量．
练习册系列答案
阅读快车系列答案
相关题目
设i为虚数单位，则复数（
）2003+（
）2004等于（ ）
| 1+i |
| 1-i |
| 1-i |
| 1+i |
| A、1+i | B、1-i |
| C、-1+i | D、-1-i |
一个侧棱与底面垂直的棱柱被一个平面截去一部分后所剩几何体的三视图如图所示，则截去那一部分的体积为．（ ）| A、1 | ||
B、
| ||
| C、11 | ||
| D、12 |
已知集合A={x|x2-1≥0}，集合B={x|x-1≤0}，则（∁RA）∩B=（ ）
| A、{x|x≥1} |
| B、{x|-1＜x＜1} |
| C、{x|-1x≤1} |
| D、{x|x＜-1} |
下列命题正确的是（ ）
A、
| ||||||||
| B、对任意的实数x，都有x3≥x2-x+1恒成立． | ||||||||
C、y=
| ||||||||
| D、y=2x（2-x），（x≥2）的最大值为2 |