题目内容

已知向量
a
=（1，1），b=（x2，x+2），若
a
，
b
共线，则实数x的值为（　　）
A、-1B、2
C、-1或2D、1或-2
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用向量共线的坐标关系得到x的等式解之．
解答： 解：因为
a
，
b
共线，向量
a
=（1，1），b=（x2，x+2），所以x2=x+2，解得x=-1或者x=2；
故选：C．
点评：本题考查了向量共线的坐标关系；属于基础题目．
练习册系列答案
相关题目
复数
a+i
2-i
为纯虚数，则实数a=（　　）
A、-2
B、-
1
2
C、2
D、
1
2
已知抛物线C：x2=4y的焦点为F，准线为l，A是l上一点，B是直线AF与C的一个交点，若
FA
=-4
FB
，则|BF|=（　　）
A、
3
2
B、
5
2
C、3
D、5
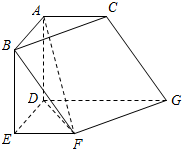在如图所示的几何体中，四边形ABED是矩形，四边形ADGC是梯形，AD⊥平面DEFG，EF∥DG，∠EDG=120°．AB=AC=FE=1，DG=2．
（Ⅰ）求证：AE∥平面BFGC；
（Ⅱ）求证：FG⊥平面ADF．
如图是长和宽分别相等的两个矩形，给定下列四个命题：
①存在三棱柱，其正视图、侧视图如图；
②存在四棱柱，其俯视图与其中一个视图完全一样；
③存在圆柱，其正视图、侧视图如图；
④若矩形的长与宽分别是2和1，则该几何体的最大体积为4．
其中真命题的个数是（　　）
A、4B、3C、2D、1
已知三个数x-a，x，x+a，若f（x）=f（x+a）+f（x-a），则f（x）的一个周期T=
 

注：f（x）=f（x+a）+f（x-a）?f（x+3a）+f（x）=0?f（x）=f（x+6a）
双曲线
x2
a2
-
y2
b2
=1与椭圆
x2
m2
+
y2
b2
=1（a＞0，m＞b＞0）的离心率互为倒数，则（　　）
A、a2+b2=m2
B、a+b=m
C、a2=b2+m2
D、a=b+m
设函数f（x）=x2ex-1-
1
3
x3-x2（x∈R）．
（1）求函数f（x）的单调区间；
（2）当x∈（1，+∞）时，用数学归纳法证明：?n∈N*，ex-1＞
xn
n!
（其中n!=1×2×…×n）．
双曲线
x2
16
-
y2
9
=1的渐近线方程为（　　）
A、y=±
4
3
x
B、y=±
3
4
x
C、y=±
3
5
x
D、y=±
4
5
x

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网