题目内容
已知抛物线C:x2=4y的焦点为F,准线为l,A是l上一点,B是直线AF与C的一个交点,若
=-4
,则|BF|=( )
| FA |
| FB |
A、
| ||
B、
| ||
| C、3 | ||
| D、5 |
考点:抛物线的简单性质
专题:计算题,平面向量及应用,圆锥曲线的定义、性质与方程
分析:由抛物线的焦点坐标和准线方程,设出A,B的坐标,得到向量FA,FB的坐标,由向量共线的坐标关系,以及抛物线的定义,即可求得.
解答:
解:抛物线C:x2=4y的焦点为F(0,1),准线为l:y=-1,
设A(a,-1),B(m,n),则
=(a,-2),
=(m,n-1),
∵
=-4
,
∴-2=-4(n-1),
∴n=
,
∴由抛物线的定义可得|BF|=n+1=
故选B.
设A(a,-1),B(m,n),则
| FA |
| FB |
∵
| FA |
| FB |
∴-2=-4(n-1),
∴n=
| 3 |
| 2 |
∴由抛物线的定义可得|BF|=n+1=
| 5 |
| 2 |
故选B.
点评:本题考查抛物线的定义和性质,考查向量知识的运用,考查学生的计算能力,属于基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
已知幂函数y=f(x)的图象过点(
,
),则f(2)=( )
| 1 |
| 2 |
| ||
| 2 |
A、-
| ||
B、
| ||
| C、-2 | ||
| D、2 |
有下列四个命题
①“若x+y=0,则x,y互为相反数”的否命题
②“若q>1则x2+2x+q=0有实根“的逆否命题
③”tanα=tanβ,则α=β”的逆命题
④若x≠2且y≠1,则x+y≠3
其中真命题为( )
①“若x+y=0,则x,y互为相反数”的否命题
②“若q>1则x2+2x+q=0有实根“的逆否命题
③”tanα=tanβ,则α=β”的逆命题
④若x≠2且y≠1,则x+y≠3
其中真命题为( )
| A、①② | B、①③ | C、①④ | D、① |
已知向量
=(1,1),b=(x2,x+2),若
,
共线,则实数x的值为( )
| a |
| a |
| b |
| A、-1 | B、2 |
| C、-1或2 | D、1或-2 |
甲、乙两人向同一目标射击,命中率分别为0.4、0.5,则恰有一人命中的概率为( )
| A、0.9 | B、0.2 |
| C、0.7 | D、0.5 |
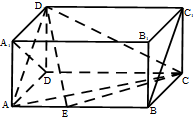 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动