题目内容
已知O为△ABC的外心,AB=4,AC=2,∠BAC=120°.若
=λ1
+λ2
,则λ1+λ2= .
| AO |
| AB |
| AC |
考点:向量加减混合运算及其几何意义
专题:平面向量及应用
分析:通过建立直角坐标系,利用相互垂直的直线斜率之间的关系、外心的性质可得外心O的坐标,再利用向量的坐标运算及其相等即可得出.
解答:
解:如图:以A为原点,以AB所在的直线为x轴,建立直角系:
则A(0,0),B (4,0),C(-1,
)),
∵O为△ABC的外心,
∴O在AB的中垂线 m:x=2 上,又在AC的中垂线 n 上,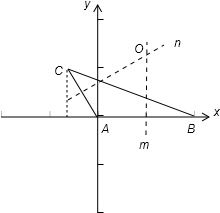
AC的中点(-
,
),∵kAC=-
,
∴得到直线AC的垂直平分线n的斜率kn=
.
其方程为:y-
=
(x+
).化为y=
x+
.
把x=2代入上述方程可得:y=
.
∴外心O(2,
).
∵
=λ1
+λ2
,
∴(2,
)=λ1(4,0)+λ2(-1,
),
∴
,解得λ2=
,λ1=
.
∴λ1+λ2=
.
故选为:
.
则A(0,0),B (4,0),C(-1,
| 3 |
∵O为△ABC的外心,
∴O在AB的中垂线 m:x=2 上,又在AC的中垂线 n 上,

AC的中点(-
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴得到直线AC的垂直平分线n的斜率kn=
| ||
| 3 |
其方程为:y-
| ||
| 2 |
| ||
| 3 |
| 1 |
| 2 |
| ||
| 3 |
| 2 |
| 3 |
| 3 |
把x=2代入上述方程可得:y=
| 4 |
| 3 |
| 3 |
∴外心O(2,
4
| ||
| 3 |
∵
| AO |
| AB |
| AC |
∴(2,
4
| ||
| 3 |
| 3 |
∴
|
| 4 |
| 3 |
| 5 |
| 6 |
∴λ1+λ2=
| 13 |
| 6 |
故选为:
| 13 |
| 6 |
点评:本题考查了相互垂直的直线斜率之间的关系、外心的性质、向量的坐标运算及其相等、平面向量基本定理,属于中档题题.

练习册系列答案
相关题目
若a,b∈R,则以下命题为真的是( )
A、若a>b,则
| ||||
B、若a>|b|,则
| ||||
| C、若a>b,则a2>b2 | ||||
| D、若a>|b|,则a2>b2 |
已知函数F(x)=ex满足F(x)=g(x)+h(x),且g(x),h(x)分别是R上的偶函数和奇函数,若?x∈[1,2]使得不等式g(2x)-ah(x)≥0恒成立,则实数a的取值范围是( )
A、(-∞,2
| ||
B、(-∞,2
| ||
C、(0,2
| ||
D、(2
|