题目内容
对于任意实数x,不等式|2x+m|+|x-1|≥a恒成立时,若实数a的最大值为3,则实数m的值为
.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:由题意可得|2x+m|+|x-1|的最小值为3,设f(x)=|2x+m|+|x-1|=2|x+
|+|x-1|,分①当
≥-1时,
②当
<-1时两种情况,分别求得f(x)的最小值,再根据函数的最小值为3求得实数m的范围.
| m |
| 2 |
| m |
| 2 |
②当
| m |
| 2 |
解答:
 解:不等式|2x+m|+|x-1|≥a恒成立时,
解:不等式|2x+m|+|x-1|≥a恒成立时,
由于实数a的最大值为3,
则|2x+m|+|x-1|的最小值为3.
设f(x)=|2x+m|+|x-1|=2|x+
|+|x-1|,
①当
≥-1时,
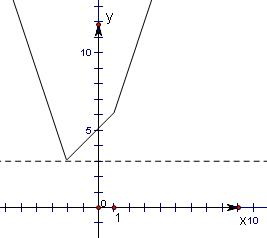
则有f(x)=
,
其图象如图所示,当x=-
时,
取得最小值f(-
)=
+1;
②当
<-1时,
则有f(x)=
,
当x=-
时,取得最小值f(-
)=-
-1;
由题意,若实数a的最大值为3,则
+1=3或-
-1=3,
∴m=4,或m=-8.
故答案为:4或-8.
 解:不等式|2x+m|+|x-1|≥a恒成立时,
解:不等式|2x+m|+|x-1|≥a恒成立时,由于实数a的最大值为3,
则|2x+m|+|x-1|的最小值为3.
设f(x)=|2x+m|+|x-1|=2|x+
| m |
| 2 |
①当
| m |
| 2 |
则有f(x)=
|
其图象如图所示,当x=-
| m |
| 2 |
取得最小值f(-
| m |
| 2 |
| m |
| 2 |
②当
| m |
| 2 |
则有f(x)=
|
当x=-
| m |
| 2 |
| m |
| 2 |
| m |
| 2 |
由题意,若实数a的最大值为3,则
| m |
| 2 |
| m |
| 2 |
∴m=4,或m=-8.
故答案为:4或-8.
点评:本题主要考查绝对值不等式的解法,以及恒成立问题,体现了等价转化的数学思想,属于中档题.

练习册系列答案
相关题目
已知l、m是两条不同的直线,a是个平面,则下列命题正确的是( )
| A、若l∥a,m∥a,则l∥m |
| B、若l⊥m,m∥a,则l⊥a |
| C、若l⊥m,m⊥a,则l∥a |
| D、若l∥a,m⊥a,则l⊥m |