题目内容
已知函数f(x)=-x2+8x,g(x)=x-ln(x+1)
(Ⅰ)求f(x)在区间[t,t+1]上的最大值h(t);
(Ⅱ)是否存在实数k,对任意的x∈[0,+∞),不等式g(x)≤8kx-kf(x)恒成立?若存在,求出k的取值范围;若不存在,说明理由.
(Ⅰ)求f(x)在区间[t,t+1]上的最大值h(t);
(Ⅱ)是否存在实数k,对任意的x∈[0,+∞),不等式g(x)≤8kx-kf(x)恒成立?若存在,求出k的取值范围;若不存在,说明理由.
考点:函数恒成立问题,二次函数在闭区间上的最值
专题:函数的性质及应用
分析:(Ⅰ)根据二次函数的单调性和对称轴之间的关系,即可求f(x)在区间[t,t+1]上的最大值h(t);
(Ⅱ)利用导数将不等式恒成立转化为求函数最值问题.
(Ⅱ)利用导数将不等式恒成立转化为求函数最值问题.
解答:
解:(Ⅰ)f(x)=-x2+8x=-(x-4)2+16.
当t+1<4,即t<3时,f(x)在[t,t+1]上单调递增,h(t)=f(t+1)=-(t+1)2+8(t+1)=-t2+6t+7;
当t≤4≤t+1,即3≤t≤4时,h(t)=f(4)=16;
当t>4时,f(x)在[t,t+1]上单调递减,h(t)=f(t)=-t2+8t.
综上,h(t)=
.
(Ⅱ)∵g(x)≤8kx-kf(x),
∴不等式等价为8kx-kf(x)-g(x)≤0,
设h(x)=8kx-kf(x)-g(x)=kx2-x+ln(x+1),x≥0
则h(x)≥0在x∈[0,+∞),上恒成立,?h(x)min≥0,
h/(x)=2kx+
-1=
,
①k≤0时,h′(x)<0,h(x)在[0,+∞)上减函数,h(x)≤h(0)=0;
∴不等式g(x)≤8kx-kf(x)不恒成立;不合题意.
②当0<k<
时,h/(x)=2kx+
-1=
=
,
当x∈(0,
)时,h′(x)<0,存在x0∈(0,
),使h(x0)<h(0)=0,
∴g(x0)>8kx0-kf(x0),
∴x∈[0,+∞)不等式g(x)≤8kx-kf(x)不恒成立,
③当k≥
时,h′(x)>0,h(x)在x∈[0,+∞)上为增函数,
∴h(x)≥h(0)=0;符合题意;
综上:存在k∈[
,+∞)对任意的x∈[0,+∞),不等式g(x)≤8kx-kf(x)恒成立.
当t+1<4,即t<3时,f(x)在[t,t+1]上单调递增,h(t)=f(t+1)=-(t+1)2+8(t+1)=-t2+6t+7;
当t≤4≤t+1,即3≤t≤4时,h(t)=f(4)=16;
当t>4时,f(x)在[t,t+1]上单调递减,h(t)=f(t)=-t2+8t.
综上,h(t)=
|
(Ⅱ)∵g(x)≤8kx-kf(x),
∴不等式等价为8kx-kf(x)-g(x)≤0,
设h(x)=8kx-kf(x)-g(x)=kx2-x+ln(x+1),x≥0
则h(x)≥0在x∈[0,+∞),上恒成立,?h(x)min≥0,
h/(x)=2kx+
| 1 |
| x+1 |
| 2kx2+2kx-x |
| x+1 |
①k≤0时,h′(x)<0,h(x)在[0,+∞)上减函数,h(x)≤h(0)=0;
∴不等式g(x)≤8kx-kf(x)不恒成立;不合题意.
②当0<k<
| 1 |
| 2 |
| 1 |
| x+1 |
| 2kx2+2kx-x |
| x+1 |
2kx(x-
| ||
| x+1 |
当x∈(0,
| 1-2k |
| 2k |
| 1-2k |
| 2k |
∴g(x0)>8kx0-kf(x0),
∴x∈[0,+∞)不等式g(x)≤8kx-kf(x)不恒成立,
③当k≥
| 1 |
| 2 |
∴h(x)≥h(0)=0;符合题意;
综上:存在k∈[
| 1 |
| 2 |
点评:本题主要考查一元二次函数的图象和性质,以及不等式恒成立问题,将不等式恒成立转化为函数最值问题是解决本题的关键.

练习册系列答案
相关题目
一个几何体的三视图如图所示,则该几何体的表面积是( )
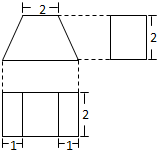

A、18+2
| ||
B、24+2
| ||
C、24+4
| ||
D、36+4
|