题目内容
2.函数f(a)=cos2θ+acosθ-a(a∈[1,2],θ∈[$\frac{π}{6}$,$\frac{π}{3}$])的最小值是$\frac{1-2a}{4}$.分析 先化简函数的解析式,利用余弦函数的定义域和值域求得cosθ的范围,结合二次函数的性质,求得函数的最小值.
解答 解:∵函数f(a)=cos2θ+acosθ-a=${(cosθ+\frac{a}{2})}^{2}$-a-$\frac{{a}^{2}}{4}$,a∈[1,2],θ∈[$\frac{π}{6}$,$\frac{π}{3}$],
∴$\frac{a}{2}$∈[$\frac{1}{2}$,1],cosθ∈[$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$],故当cosθ=$\frac{1}{2}$时,f(a)取得最小值为 $\frac{1-2a}{4}$,
故答案为:$\frac{1-2a}{4}$.
点评 本题主要考查余弦函数的定义域和值域,二次函数的性质,属于中档题.

练习册系列答案
相关题目
1. 某超市连锁店统计了城市甲、乙的各16台自动售货机在中午12:00至13:00间的销售金额,并用茎叶图表示如图.则有( )
某超市连锁店统计了城市甲、乙的各16台自动售货机在中午12:00至13:00间的销售金额,并用茎叶图表示如图.则有( )
 某超市连锁店统计了城市甲、乙的各16台自动售货机在中午12:00至13:00间的销售金额,并用茎叶图表示如图.则有( )
某超市连锁店统计了城市甲、乙的各16台自动售货机在中午12:00至13:00间的销售金额,并用茎叶图表示如图.则有( )| A. | 甲城销售额多,乙城不够稳定 | B. | 甲城销售额多,乙城稳定 | ||
| C. | 乙城销售额多,甲城稳定 | D. | 乙城销售额多,甲城不够稳定 |
2.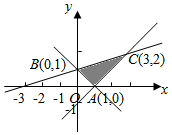 设x,y满足如图所示的可行域(阴影部分),则$z=\frac{1}{2}x-y$的最大值为( )
设x,y满足如图所示的可行域(阴影部分),则$z=\frac{1}{2}x-y$的最大值为( )
 设x,y满足如图所示的可行域(阴影部分),则$z=\frac{1}{2}x-y$的最大值为( )
设x,y满足如图所示的可行域(阴影部分),则$z=\frac{1}{2}x-y$的最大值为( )| A. | $\frac{1}{2}$ | B. | 0 | C. | $-\frac{1}{2}$ | D. | -1 |
11.若a<b<0,则下列不等式成立的是( )
| A. | a2<b2 | B. | ab<b2 | C. | ab>a2 | D. | $a-\frac{1}{a}<b-\frac{1}{b}$ |
 如图,在四棱锥P-ABCD中,侧棱长均相等且为$\sqrt{2}$,DA=DC=$\sqrt{3}$,AB=BC=1.
如图,在四棱锥P-ABCD中,侧棱长均相等且为$\sqrt{2}$,DA=DC=$\sqrt{3}$,AB=BC=1.