题目内容
解关于x的方程：x2+ax+
（a2+3）=x2+x+1．
| 1 |
| 4 |
考点：二次函数的性质
专题：函数的性质及应用
分析：原方程化简为可得 （a-1）[x+
]=0，再分当a=1时、当a≠1时两种情况，分别求得方程的解集．
| a+1 |
| 4 |
解答：
解：由关于x的方程：x2+ax+
（a2+3）=x2+x+1，可得 （a-1）[x+
]=0，
当a=1时，方程的解集为R．
当a≠1时，方程的解集为{x|x=-
}．
| 1 |
| 4 |
| a+1 |
| 4 |
当a=1时，方程的解集为R．
当a≠1时，方程的解集为{x|x=-
| a+1 |
| 4 |
点评：本题主要考查一次方程的解法，体现了分类讨论的数学思想，属于基础题．
练习册系列答案
备战中考寒假系列答案
相关题目
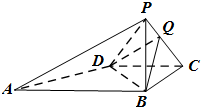已知四面体P-ABCD中，PB⊥平面ABCD，底面ABCD是直角梯形，∠ABC=∠BCD=90°，PB=BC=CD=