题目内容
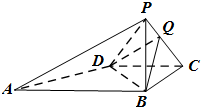 已知四面体P-ABCD中,PB⊥平面ABCD,底面ABCD是直角梯形,∠ABC=∠BCD=90°,PB=BC=CD=
已知四面体P-ABCD中,PB⊥平面ABCD,底面ABCD是直角梯形,∠ABC=∠BCD=90°,PB=BC=CD=| 1 |
| 2 |
(1)求证:平面PAD⊥面PBD;
(2)当Q在什么位置时,PA∥平面QBD?
考点:平面与平面垂直的判定,直线与平面平行的性质
专题:空间位置关系与距离
分析:(1)由已知条件推导出AD⊥BD,PB⊥AD,从而得到AD⊥平面PBD,由此能证明平面PAD⊥平面PBD.
(2)当PQ=2QC时,PA∥平面QBD.连结AC交BD于点O,连接OQ,由已知条件得AO=2OC,所以由AP∥OQ,得到PQ=2QC.
(2)当PQ=2QC时,PA∥平面QBD.连结AC交BD于点O,连接OQ,由已知条件得AO=2OC,所以由AP∥OQ,得到PQ=2QC.
解答:
(1)证明:∵∠ABC=∠BCD=90°,BC=CD=
AB,
设BC=1,则AD=BD=
,
∴AD2+BD2=AB2,∴AD⊥BD,
又PB⊥平面ABCD.∴PB⊥AD
又因为BD,PB在平面PBD内,且BD与PB相交,
∴AD⊥平面PBD
又AD?面PAD,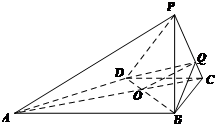
∴平面PAD⊥平面PBD.…(6分)
(2)解:当PQ=2QC时,PA∥平面QBD.
证明如下,连结AC交BD于点O,连接OQ,
∵2CD=AB,CD∥AB,∴AO=2OC
过PA的平面PAC∩平面QBD=OQ,
∵PA∥平面QBD,∴AP∥OQ,∴PQ=2QC.…(12分)
| 1 |
| 2 |
设BC=1,则AD=BD=
| 2 |
∴AD2+BD2=AB2,∴AD⊥BD,
又PB⊥平面ABCD.∴PB⊥AD
又因为BD,PB在平面PBD内,且BD与PB相交,
∴AD⊥平面PBD
又AD?面PAD,

∴平面PAD⊥平面PBD.…(6分)
(2)解:当PQ=2QC时,PA∥平面QBD.
证明如下,连结AC交BD于点O,连接OQ,
∵2CD=AB,CD∥AB,∴AO=2OC
过PA的平面PAC∩平面QBD=OQ,
∵PA∥平面QBD,∴AP∥OQ,∴PQ=2QC.…(12分)
点评:本题考查平面与平面垂直的判断,考查直线与平面平行时点的位置的确定,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目