题目内容
已知点F1(-1,0),F2(1,0)分别是椭圆C:
+
=1(a>b>0)的左、右焦点,点P(1,
)在椭圆上C上.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设直线l1:y=kx+m,l2:y=kx-m,若l1、l2均与椭圆C相切,试探究在x轴上是否存在定点M,点M到l1,l2的距离之积恒为1?若存在,请求出点M坐标;若不存在,请说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设直线l1:y=kx+m,l2:y=kx-m,若l1、l2均与椭圆C相切,试探究在x轴上是否存在定点M,点M到l1,l2的距离之积恒为1?若存在,请求出点M坐标;若不存在,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(I)由题意可知:
,解得即可.
(II)把直线l1的方程与椭圆的方程联立可得(1+2k2)x2+4mkx+2m2-2=0,由于直线与椭圆相切,可得△=0,m2=1+2k2.设M(t,0),利用点到直线的距离公式可得m,k,t的关系式,代入星期日m即可得出t的值.
|
(II)把直线l1的方程与椭圆的方程联立可得(1+2k2)x2+4mkx+2m2-2=0,由于直线与椭圆相切,可得△=0,m2=1+2k2.设M(t,0),利用点到直线的距离公式可得m,k,t的关系式,代入星期日m即可得出t的值.
解答:
解:(I)由题意可知:
,解得b=c=1,a2=2.
∴椭圆C的标准方程为
+y2=1.
(II)把直线l1的方程与椭圆的方程联立可得
,
化为(1+2k2)x2+4mkx+2m2-2=0,
∵直线l1与椭圆相切,∴△=16m2k2-4(1+2k2)(2m2-2)=0,化为m2=1+2k2.
同理把直线l2的方程与椭圆的方程联立也可得m2=1+2k2.
假设存在定点M(t,0)满足条件,则
•
=1,
化为|k2t2-m2|=1+k2,
把m2=1+2k2代入上式化为k2(t2-3)=2或k2(t2-1)=0.
其中k2(t2-3)=2不是对于任意k恒成立,应舍去.
由k2(t2-1)=0对于任意k恒成立,可得t=±1.
综上可知:满足题意的点M存在,为(±1,0).
|
∴椭圆C的标准方程为
| x2 |
| 2 |
(II)把直线l1的方程与椭圆的方程联立可得
|
化为(1+2k2)x2+4mkx+2m2-2=0,
∵直线l1与椭圆相切,∴△=16m2k2-4(1+2k2)(2m2-2)=0,化为m2=1+2k2.
同理把直线l2的方程与椭圆的方程联立也可得m2=1+2k2.
假设存在定点M(t,0)满足条件,则
| |kt+m| | ||
|
| |kt-m| | ||
|
化为|k2t2-m2|=1+k2,
把m2=1+2k2代入上式化为k2(t2-3)=2或k2(t2-1)=0.
其中k2(t2-3)=2不是对于任意k恒成立,应舍去.
由k2(t2-1)=0对于任意k恒成立,可得t=±1.
综上可知:满足题意的点M存在,为(±1,0).
点评:本题主要考查了椭圆的定义及其标准方程、直线与椭圆的位置关系,考查了分析问题和解决问题的能力,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
 给定两个平面向量
给定两个平面向量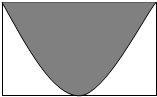 如图,长方形的面积为2,将100颗豆子随机地撒在长方形内,其中恰好有60颗豆子落在阴影部分内,则用随机摸拟的方法可以估计图中阴影部分的面积为( )
如图,长方形的面积为2,将100颗豆子随机地撒在长方形内,其中恰好有60颗豆子落在阴影部分内,则用随机摸拟的方法可以估计图中阴影部分的面积为( )