题目内容

记集合A={（x，y）|x2+y2≤4}和集合B={（x，y）|x+y-2≤0，x≥0，y≥0}表示的平面区域分别为Ω1和Ω2，若在区域Ω1内任取一点M（x，y），则点M落在区域Ω2的概率为
 
．
考点：几何概型
专题：概率与统计
分析：分别求出集合A，B对应区域的面积，根据几何概型的概率公式即可得到结论．
解答： 解：区域Ω1对应的面积S1=4π，
作出平面区域Ω2，
则Ω2对应的平面区域如图为△OAB：
则对应的面积S=
1
2
×2×2=2，
则根据几何概型的概率公式可知若在区域Ω1内任取一点M（x，y），则点M落在区域Ω2的概率为
2
4π
=
1
2π
，
故答案是：
1
2π
．
点评：本题主要考查几何概型的概率公式的计算，根据条件求出相应的面积是解决本题的关键．
练习册系列答案
相关题目
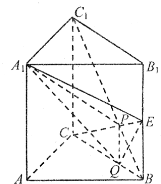如图在直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=
3
，AA1=2，E是BB1的中点，且CE交BC1于点P，点Q在线段BC上，CQ=2QB．
（1）证明：CC1∥平面A1PQ；
（2）若直线BC⊥平面A1PQ，求二面角A1-QE-P的大小．
已知函数f（x）=ln（1+x）-x+
k
2
x2，（k＞0，且k≠1）．
（Ⅰ）当k=2时，求曲线y=f（x）在点（1，f（1））处的切线方程；
（Ⅱ）求f（x）的单调减区间；
（Ⅲ）当k=0时，设f（x）在区间[0，n]（n∈N*）上的最小值为bn，令an=ln（1+n）-bn，
求证：
a1
a2
+
a1a3
a2a4
+…+
a1a3…a2n-1
a2a4..a2n
＜
2an+1
-1，（n∈N*）．
已知点F1（-1，0），F2（1，0）分别是椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点，点P（1，
2
2
）在椭圆上C上．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）设直线l1：y=kx+m，l2：y=kx-m，若l1、l2均与椭圆C相切，试探究在x轴上是否存在定点M，点M到l1，l2的距离之积恒为1？若存在，请求出点M坐标；若不存在，请说明理由．
已知f（x）、g（x）都是定义在R上的函数，g（x）≠0，f′（x）g（x）＜f（x）g′（x），f（x）=axg（x），
f(1)
g(1)
+
f(-1)
g(-1)
=
5
2
，则关于x的方程abx2+
2
x+
5
2
=0（b∈（0，1））有两个不同实根的概率为
 
．
如图，PA与圆O相切于A，不过圆心O的割线PCB与直径AE相交于D点．已知∠BPA=30°，AD=2，PC=1，则圆O的半径等于
 
．
设函数f（x）=x|x|+bx+c，给出四个命题：上述四个命题中所有正确的命题序号是
 
．
①c=0时，有f（-x）=-f（x）成立；
②b=0，c＞0时，函数y=f（x）只有一个零点；
③y=f（x）的图象关于点（0，c）对称；
④函数y=f（x），至多有两个不同零点．
已知甲盒内有大小相同的1个红球和3个黑球，乙盒内有大小相同的2个红球和4个黑球．现从甲、乙两个盒内各任取2个球．设ξ为取出的4个球中红球的个数，则ξ的数学期望Eξ=
 
．
下列四个命题中正确的命题序号是（　　）
①向量
a
，
b
共线的充分必要条件是存在唯一实数λ，使
a
=λ
b
成立．
②函数y=f（x-1）与y=f（1-x）的图象关于直线x=1对称．
③ysinθ-cosθ=2y（θ∈[0，π]）成立的充分必要条件是|2y|≤
1+y2
．
④已知U为全集，则x∉A∩B的充分条件是x∈（∁UA）∩（∁UB）．
A、②④B、①②C、①③D、③④

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网