题目内容
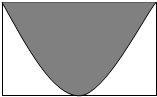如图，长方形的面积为2，将100颗豆子随机地撒在长方形内，其中恰好有60颗豆子落在阴影部分内，则用随机摸拟的方法可以估计图中阴影部分的面积为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
考点：几何概型
专题：概率与统计
分析：根据几何概型的概率公式，可以求出豆子落在阴影部分的概率，然后即可得到阴影部分的面积．
解答：
解：将100颗豆子随机地撒在长方形内，其中恰好有60颗豆子落在阴影部分内，
则豆子落在阴影部分的概率P=
=
，
∵长方形的面积为2，
∴阴影部分的面积S，满足
=
，即S=
，
故选：C
则豆子落在阴影部分的概率P=
| 60 |
| 100 |
| 3 |
| 5 |
∵长方形的面积为2，
∴阴影部分的面积S，满足
| S |
| 2 |
| 3 |
| 5 |
| 6 |
| 5 |
故选：C
点评：本题主要考查几何概型的应用，根据面积之间的关系是解决本题的关键，比较基础．
练习册系列答案
相关题目
假设在时间间隔T内的任何时刻，两条不相关的短信机会均等地进入同一台手机．若这两条短信进入手机的间隔时间不大于t（0＜t＜T）称手机受到干扰，则手机受到干扰的概率是（ ）
A、（
| ||
B、（1-
| ||
C、1-（
| ||
D、1-（1-
|
函数函数y=sin（3x+
）cos（x-
）+cos（3x+
）sin（x-
）的图象的一条对称轴的方程是（ ）
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
A、x=-
| ||
B、x=-
| ||
C、x=
| ||
D、x=
|
下列说法正确的是（ ）
| A、直角坐标系中横、纵坐标相等的点能够组成一个集合 |
| B、π∈{x|x＜3，x∈R} |
| C、∅={0} |
| D、{（1，2）}⊆{1，2，3} |
已知集合M={x|x＜1}，集合N={y|y＞0}，则M∩N=（ ）
| A、{x|x＜1} |
| B、{x|x＞1} |
| C、{x|0＜x＜1} |
| D、∅ |