题目内容
在集合{(x,y)|
}所表示的平面区域内任取一点M,则点M恰好取自x轴上方的概率为 .
|
考点:几何概型
专题:综合题,概率与统计
分析:作出可行域,计算出面积,即可求出点M恰好取自x轴上方的概率.
解答:
 解:如图所示,A(1,1),C(1.5,0),B(3,-3),则
解:如图所示,A(1,1),C(1.5,0),B(3,-3),则
S△AOC=
•1.5•1=
,S△AOB=
+
•1.5•3=3,
∴点M恰好取自x轴上方的概率为
=
.
故答案为:
.
 解:如图所示,A(1,1),C(1.5,0),B(3,-3),则
解:如图所示,A(1,1),C(1.5,0),B(3,-3),则S△AOC=
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
∴点M恰好取自x轴上方的概率为
| ||
| 3 |
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:本题考查几何概型的概率,可以为长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
若cos2t=-
cosxdx,其中t∈(0,π),则t=( )
| ∫ | t 0 |
A、
| ||
B、
| ||
C、
| ||
| D、π |
若平面内两个向量
=(2cosθ,1)与
=(1,cosθ)共线,则cos2θ等于( )
| a |
| b |
A、
| ||
| B、1 | ||
| C、-1 | ||
| D、0 |
如图是甲,乙两名同学5次综合测评成绩的茎叶图,下列四个结论中,正确的是( )
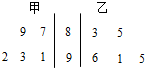

| A、甲成绩的极差大于乙成绩的极差 |
| B、甲成绩的中位数小于乙成绩的中位数 |
| C、甲成绩的平均值等于乙成绩的平均值 |
| D、甲成绩的标准差小于乙成绩的标准差 |
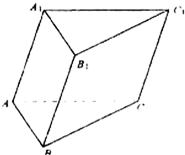 如图,用四种不同颜色给三棱柱ABC-A1B1C1的六个顶点涂色,要求四种颜色全都用上,每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色.则不同的涂色方法的种数为
如图,用四种不同颜色给三棱柱ABC-A1B1C1的六个顶点涂色,要求四种颜色全都用上,每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色.则不同的涂色方法的种数为