题目内容
14.已知函数f(x)=2sin(ωx+φ-$\frac{π}{6}$)+1(0<φ<π,ω>0)为偶函数,且f(x)图象的两对称轴间的距离为$\frac{π}{3}$.(1)求f($\frac{π}{6}$)的值;
(2)求函数f(x)的对称轴方程和对称中心;
(3)当x∈[-$\frac{π}{6}$,$\frac{π}{2}$]求函数f(x)的值域.
分析 (1)由条件利用诱导公式、正弦函数的奇偶性、周期性,求得φ和ω的值,可得函数的解析式,从而求得f($\frac{π}{6}$)的值.
(2)由条件利用余弦函数的图象的对称性,求得函数f(x)的对称轴方程和对称中心.
(3)由x∈[-$\frac{π}{6}$,$\frac{π}{2}$],利用余弦函数的定义域和值域,求得函数f(x)的值域.
解答 解:(1)∵函数f(x)=2sin(ωx+φ-$\frac{π}{6}$)+1(0<φ<π,ω>0)为偶函数,
∴φ-$\frac{π}{6}$=$\frac{π}{2}$,φ=$\frac{2π}{3}$.
由f(x)图象的两对称轴间的距离为$\frac{π}{3}$,可得$\frac{1}{2}$•$\frac{2π}{ω}$=$\frac{π}{3}$,求得ω=3,
故f(x)=2sin(3x+$\frac{π}{2}$)+1=2cos3x+1.
∴f($\frac{π}{6}$)=2cos$\frac{π}{2}$+1=1.
(2)令3x=kπ,求得x=$\frac{kπ}{3}$,k∈Z,故函数f(x)的对称轴方程为x=$\frac{kπ}{3}$,k∈Z;
令3x=kπ+$\frac{π}{2}$,求得x=$\frac{kπ}{3}$+$\frac{π}{6}$,k∈Z,故函数f(x)的对称中心为($\frac{kπ}{3}$+$\frac{π}{6}$,0),k∈Z.
(3)当x∈[-$\frac{π}{6}$,$\frac{π}{2}$],3x∈[-$\frac{π}{2}$,$\frac{3π}{2}$],∴cos3x∈[-1,1],
∴f(x)=2cos3x+1∈[-1,3],故函数f(x)的值域为[-1,3].
点评 本题主要考查正弦函数的奇偶性、周期性,余弦函数的图象的对称性,余弦函数的定义域和值域,属于基础题.

| A. | 2 | B. | 3 | C. | 9 | D. | 11 |
| A. | (-1,1),2 | B. | (-1,1),4 | C. | [-1,1],2 | D. | [-1,1],4 |
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
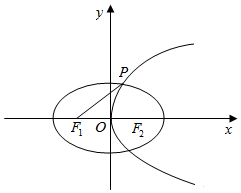 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点分别为F1,F2,抛物线y2=4x与椭圆C有相同的焦点,点P为抛物线与椭圆C在第一象限的交点,且|PF1|=$\frac{7}{3}$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点分别为F1,F2,抛物线y2=4x与椭圆C有相同的焦点,点P为抛物线与椭圆C在第一象限的交点,且|PF1|=$\frac{7}{3}$.