题目内容
2.方程πx(x+$\frac{x}{π}$-1)=2x-1实数解的个数为2个.分析 化简可得πx-1=$\frac{2}{π+1}$+$\frac{\frac{2π}{π+1}-1}{(π+1)x-π}$,作函数y=πx-1与y=$\frac{2}{π+1}$+$\frac{\frac{2π}{π+1}-1}{(π+1)x-π}$的图象,从而解得.
解答 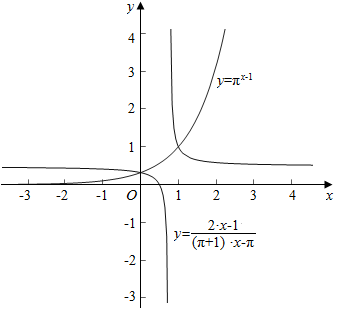 解:∵πx(x+$\frac{x}{π}$-1)=2x-1,
解:∵πx(x+$\frac{x}{π}$-1)=2x-1,
∴πx(x$\frac{π+1}{π}$-1)=2x-1,
∴x≠$\frac{π}{π+1}$,
且πx-1=$\frac{2x-1}{(π+1)x-π}$=$\frac{2}{π+1}$+$\frac{\frac{2π}{π+1}-1}{(π+1)x-π}$,
作函数y=πx-1与y=$\frac{2}{π+1}$+$\frac{\frac{2π}{π+1}-1}{(π+1)x-π}$的图象如下,
结合图象可知,
两个函数图象有两个交点,
故答案为:2.
点评 本题考查了方程与函数的关系应用及数形结合的思想方法应用,同时考查了学生的作图能力.

练习册系列答案
相关题目
12.设集合M={x|log2(x-1)>0},集合N={x|x≥-2},则N∩∁RM=( )
| A. | {x|x≤-2} | B. | {x|-2<x≤2} | C. | {x|-2≤x≤3} | D. | {x|-2≤x≤2} |
13.若sin(θ-$\frac{π}{3}$)=$\frac{1}{3}$,0<θ<π,则cosθ=( )
| A. | $\frac{-\sqrt{3}+2\sqrt{2}}{6}$ | B. | $\frac{\sqrt{3}+2\sqrt{2}}{6}$ | C. | $\frac{-\sqrt{3}±2\sqrt{2}}{6}$ | D. | $\frac{\sqrt{3}±2\sqrt{2}}{6}$ |
8.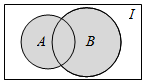 已知如图,全集I=R,集合A={x|0<x<2},B={x|1<x<3},则图中阴影部分所表示的集合为( )
已知如图,全集I=R,集合A={x|0<x<2},B={x|1<x<3},则图中阴影部分所表示的集合为( )
 已知如图,全集I=R,集合A={x|0<x<2},B={x|1<x<3},则图中阴影部分所表示的集合为( )
已知如图,全集I=R,集合A={x|0<x<2},B={x|1<x<3},则图中阴影部分所表示的集合为( )| A. | {x|0<x<2} | B. | {x|0<x<3} | C. | {x|x<3} | D. | {x|x>0} |