题目内容
已知函数f(x)=xlnx,g(x)=-
x2+
x-
(Ⅰ)求f(x)在x=e处的切线方程;
(Ⅱ)在函数f(x)与g(x)的公共定义域内f(x)的图象始终在g(x)图象的上方,求实数a的范围;
(Ⅲ)是否存在实数s,t(0<s<t),使x∈[s,t]时,函数h(x)=
+x-4图象恒在x轴上方且值域为[2lns,2lnt]?若存在,求出s,t的值,若不存在,请说明理由.
| 1 |
| 2 |
| a |
| 2 |
| 3 |
| 2 |
(Ⅰ)求f(x)在x=e处的切线方程;
(Ⅱ)在函数f(x)与g(x)的公共定义域内f(x)的图象始终在g(x)图象的上方,求实数a的范围;
(Ⅲ)是否存在实数s,t(0<s<t),使x∈[s,t]时,函数h(x)=
| 2f(x)+3 |
| x |
考点:利用导数求闭区间上函数的最值,利用导数研究曲线上某点切线方程
专题:计算题,函数的性质及应用,导数的综合应用
分析:(Ⅰ)求导f′(x)=lnx+1,f′(e)=lne+1=2,又由f(e)=e;从而写出切线方程;
(Ⅱ)函数f(x)与g(x)的公共定义域为(0,+∞);从而得x∈(0,+∞)时,f(x)-g(x)>0恒成立;即a<2lnx+x+
,从而化为函数的最值问题;
(Ⅲ)h(x)=
+x-4=2lnx+x+
-4,可知h(x)的图象在区间[s,t]上恒在x轴上方时1∉[s,t];从而分类讨论.
(Ⅱ)函数f(x)与g(x)的公共定义域为(0,+∞);从而得x∈(0,+∞)时,f(x)-g(x)>0恒成立;即a<2lnx+x+
| 3 |
| x |
(Ⅲ)h(x)=
| 2f(x)+3 |
| x |
| 3 |
| x |
解答:
解:(Ⅰ)f′(x)=lnx+1,f′(e)=lne+1=2,
又f(e)=e;
故f(x)在x=e处的切线方程为y-e=2(x-e);
故切线方程为2x-y-e=0;
(Ⅱ)函数f(x)与g(x)的公共定义域为(0,+∞);
由题意知,x∈(0,+∞)时,f(x)-g(x)>0恒成立;
即a<2lnx+x+
,
令m(x)=2lnx+x+
,
则m′(x)=
+1-
=
,
故m(x)在(0,1)上是减函数,在(1,+∞)上是增函数,
故m(x)≥m(1)=4;
故a<4;
(Ⅲ)h(x)=
+x-4
=2lnx+x+
-4,
则由(Ⅱ)知,h(x)在(0,1)上是减函数,在(1,+∞)上是增函数,
∵h(1)=0<s,且h(x)的图象在区间[s,t]上恒在x轴上方,
∴1∉[s,t];
①若0<s<t<1,则lns<0,lnt<0,不合题意;
②若1<s<t,由题意得,
;
则s,t是方程x+
-4=0的解,
而方程x+
-4=0的解为1,3;
故不合题意,
故不存在.
又f(e)=e;
故f(x)在x=e处的切线方程为y-e=2(x-e);
故切线方程为2x-y-e=0;
(Ⅱ)函数f(x)与g(x)的公共定义域为(0,+∞);
由题意知,x∈(0,+∞)时,f(x)-g(x)>0恒成立;
即a<2lnx+x+
| 3 |
| x |
令m(x)=2lnx+x+
| 3 |
| x |
则m′(x)=
| 2 |
| x |
| 3 |
| x2 |
| (x+3)(x-1) |
| x2 |
故m(x)在(0,1)上是减函数,在(1,+∞)上是增函数,
故m(x)≥m(1)=4;
故a<4;
(Ⅲ)h(x)=
| 2f(x)+3 |
| x |
=2lnx+x+
| 3 |
| x |
则由(Ⅱ)知,h(x)在(0,1)上是减函数,在(1,+∞)上是增函数,
∵h(1)=0<s,且h(x)的图象在区间[s,t]上恒在x轴上方,
∴1∉[s,t];
①若0<s<t<1,则lns<0,lnt<0,不合题意;
②若1<s<t,由题意得,
|
则s,t是方程x+
| 3 |
| x |
而方程x+
| 3 |
| x |
故不合题意,
故不存在.
点评:本题考查了导数的综合应用及恒成立问题化为最值问题的处理方法,属于中档题.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
设x=
,y=3-
,集合M={m|m=a+b
,a∈Q,b∈Q},那么x,y与集合M的关系是( )
| 1 | ||
3+2
|
| 2 |
| 2 |
| A、x∈M,y∈M |
| B、x∈M,y∉M |
| C、x∉M,y∈M |
| D、x∉M,y∉M |
设f(x)=
+2x,0<a<b<e,则( )
| lnx |
| x |
| A、f(a)>f(b) |
| B、f(a)<f(b) |
| C、f(a)=f(b) |
| D、f(a)f(b)>0 |
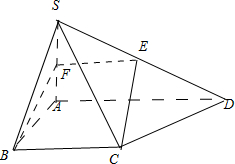 在四棱锥S-ABCD中,底面ABCD为直角梯形,其中AD∥BC,∠BAD=90°,SA⊥底面ABCD,SA=AB=BC=2,tan∠SDA=
在四棱锥S-ABCD中,底面ABCD为直角梯形,其中AD∥BC,∠BAD=90°,SA⊥底面ABCD,SA=AB=BC=2,tan∠SDA= 如图,已知斜三棱柱ABC-A1B1C1,侧面BC1是边长为3的正方形,AA1到侧面BC1的距离为2,E为侧棱CC1上一点,且C1E=1,则三棱锥E-A1B1C1的体积为
如图,已知斜三棱柱ABC-A1B1C1,侧面BC1是边长为3的正方形,AA1到侧面BC1的距离为2,E为侧棱CC1上一点,且C1E=1,则三棱锥E-A1B1C1的体积为