题目内容
3.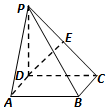 在底面是正方形的四棱锥P-ABCD中,已知PD⊥底面ABCD,且PD=CD,E为PC的中点,则异面直线PA与DE所成的角是( )
在底面是正方形的四棱锥P-ABCD中,已知PD⊥底面ABCD,且PD=CD,E为PC的中点,则异面直线PA与DE所成的角是( )| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
分析 由条件看出DA,DC,DP三直线两两垂直,从而可分别以这三直线为x,y,z轴,建立空间直角坐标系,并设DA=1,这样便可求出A,P,D,E的坐标,从而求出向量$\overrightarrow{PA},\overrightarrow{DE}$的坐标,进而求出cos$<\overrightarrow{PA},\overrightarrow{DE}>$的值,从而求出异面直线PA,DE所成的角.
解答 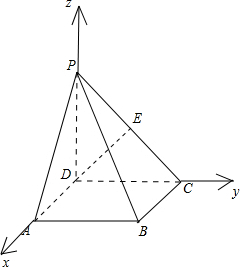 解:如图,根据条件,分别以DA,DC,DP所在直线为x,y,z轴,
解:如图,根据条件,分别以DA,DC,DP所在直线为x,y,z轴,
建立如图所示空间直角坐标系,并设DA=1,则:
DC=DP=1;
A(1,0,0),P(0,0,1),D(0,0,0),
C(0,1,0),E($0,\frac{1}{2},\frac{1}{2}$);
∴$\overrightarrow{PA}=(1,0,-1),\overrightarrow{DE}=(0,\frac{1}{2},\frac{1}{2})$;
∴$|\overrightarrow{PA}|=\sqrt{2},|\overrightarrow{DE}|=\frac{\sqrt{2}}{2}$,$\overrightarrow{PA}•\overrightarrow{DE}=-\frac{1}{2}$;
∴$cos<\overrightarrow{PA},\overrightarrow{DE}>=\frac{-\frac{1}{2}}{\sqrt{2}×\frac{\sqrt{2}}{2}}=-\frac{1}{2}$;
∴$\overrightarrow{PA},\overrightarrow{DE}$的夹角为120°;
∴异面直线PA与DE所成的角是60°.
故选B.
点评 考查建立空间直角坐标系,利用坐标,利用向量求异面直线所成角的方法,向量坐标的数量积的运算.

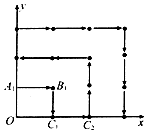 某地区为了绿化环境进行大面积植树造林,如图所示,在区域{(x,y)|x≥0,y≥0}内植树,第1棵树在点A1(0,1)处,第2棵树在点B1(1,1)处,第3棵树在点C1(1,0)处,第4棵树在点C2(2,0)处,接着按图中箭头方向每隔1个单位种1棵树.第n棵树所在点的坐标是(46,0),则n=( )
某地区为了绿化环境进行大面积植树造林,如图所示,在区域{(x,y)|x≥0,y≥0}内植树,第1棵树在点A1(0,1)处,第2棵树在点B1(1,1)处,第3棵树在点C1(1,0)处,第4棵树在点C2(2,0)处,接着按图中箭头方向每隔1个单位种1棵树.第n棵树所在点的坐标是(46,0),则n=( )| A. | 1936 | B. | 2016 | C. | 2017 | D. | 2208 |
| A. | -2tanα | B. | 2tanα | C. | $\frac{-2}{tanα}$ | D. | $\frac{2}{tanα}$ |

| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
| A. | ${x^2}+\frac{{3{y^2}}}{2}=1$ | B. | ${x^2}+\frac{{6{y^2}}}{5}=1$ | C. | ${x^2}+\frac{{5{y^2}}}{4}=1$ | D. | ${x^2}+\frac{{8{y^2}}}{7}=1$ |
| A. | 3 | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{5}$ |
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
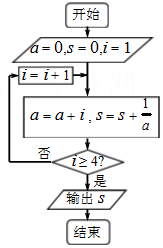
| A. | $\frac{8}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{2}$ |