题目内容
设函数f(x)=Asin(ωx+φ)(其中A>0,ω,0,-π<φ<π)在x=
处取得最大值2,其图象与x轴的相邻两个交点的距离为
,则函数f(x)的单调递增区间是 .
| π |
| 6 |
| π |
| 2 |
考点:函数y=Asin(ωx+φ)的图象变换
专题:计算题,三角函数的图像与性质
分析:先确定函数的周期,可得ω的值,利用函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,-π<φ<π)在x=
处取得最大值2,即可求得f(x)的解析式;利用正弦函数的单调性求解函数的单调增区间.
| π |
| 6 |
解答:
解:由题意,T=π,∴
=π,∴ω=2
∵函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,-π<φ<π)在x=
处取得最大值2,
∴A=2,sin(2×
+φ)=1,∴φ=
∴f(x)的解析式为f(x)=2sin(2x+
);
由-
+2kπ≤2x+
≤
+2kπ,
得-
+kπ≤x≤
+kπ,k∈Z
故所求单调增区间为[-
+kπ,
+kπ]k∈Z.
故答案为:[-
+kπ,
+kπ]k∈Z.
| 2π |
| ω |
∵函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,-π<φ<π)在x=
| π |
| 6 |
∴A=2,sin(2×
| π |
| 6 |
| π |
| 6 |
∴f(x)的解析式为f(x)=2sin(2x+
| π |
| 6 |
由-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
得-
| π |
| 3 |
| π |
| 6 |
故所求单调增区间为[-
| π |
| 3 |
| π |
| 6 |
故答案为:[-
| π |
| 3 |
| π |
| 6 |
点评:本题考查函数的解析式,考查函数的单调性,正确求函数的解析式是关键.

练习册系列答案
相关题目
函数y=sin(x-
)在区间[0,
]上( )
| π |
| 4 |
| π |
| 2 |
| A、单调递增且有最大值 |
| B、单调递增但无最大值 |
| C、单调递减且有最大值 |
| D、单调递减但无最大值 |
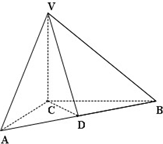 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D为AB的中点,且AC=BC=VC=a.
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D为AB的中点,且AC=BC=VC=a. 函数y=Asin(ωx+ϕ)在一个周期内的图象如图,则此函数的解析式为
函数y=Asin(ωx+ϕ)在一个周期内的图象如图,则此函数的解析式为