题目内容
函数f(x)=cos(2x-
)+
sinxcosx+
-
sin2x,下列结论中正确的有( )
①f(x)是以π为最小正周期的周期函数;
②直线x=
是函数f(x)的一条对称轴;
③f(x)在区间(0,
)上是单调增函数;
④f(x)既不是奇函数,也不是偶函数.
| π |
| 4 |
| 2 |
| ||
| 2 |
| 2 |
①f(x)是以π为最小正周期的周期函数;
②直线x=
| 3π |
| 8 |
③f(x)在区间(0,
| π |
| 2 |
④f(x)既不是奇函数,也不是偶函数.
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:命题的真假判断与应用
专题:三角函数的图像与性质
分析:利用两角和差的正弦余弦公式和倍角公式可得函数f(x)=2sin(2x+
).再利用三角函数的图象与性质即可判断出.
| π |
| 4 |
解答:
解:函数f(x)=cos(2x-
)+
sinxcosx+
-
sin2x
=
cos2x+
sin2x+
sin2x+
-
=
cos2x+
sin2x
=2sin(2x+
).
∴T=
=π,因此①正确;
sin(2×
π+
)=sinπ=0,因此直线x=
不是函数f(x)的一条对称轴,②不正确;
由x∈(0,
)可知:
<2x+
<
,可知f(x)在区间(0,
)上不是单调增函数,因此③;
f(x)既不是奇函数,也不是偶函数,故④正确.
综上可得:只有①④正确.
故选:B.
| π |
| 4 |
| 2 |
| ||
| 2 |
| 2 |
=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
=
| 2 |
| 2 |
=2sin(2x+
| π |
| 4 |
∴T=
| 2π |
| 2 |
sin(2×
| 3 |
| 8 |
| π |
| 4 |
| 3π |
| 8 |
由x∈(0,
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
| π |
| 2 |
f(x)既不是奇函数,也不是偶函数,故④正确.
综上可得:只有①④正确.
故选:B.
点评:本题考查了两角和差的正弦余弦公式、倍角公式、三角函数的图象与性质,考查了推理能力和计算能力,属于难题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
设i为虚数单位,复数Z的共轭复数为
,且(
+1)(1-i)=2i,则复数Z的模为( )
. |
| Z |
. |
| Z |
A、
| ||
| B、5 | ||
| C、-2-i | ||
| D、1 |
已知全集U=R,集合A={(x,y)|y=
},B={x|0<x≤1},则(∁UA)∪B=( )
| x2-x |
| A、(0,1) |
| B、(0,1] |
| C、(-∞,0)∪(1,+∞) |
| D、∅ |
为大力提倡“厉行节约,反对浪费”,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:
下面的临界值供参考:
x2=
,其中n*1=n11+n22,n*2=n12+n21,n1*=n11+n12,n2*=n21+n22,n=n11+n22+n12+n21
下列结论正确的是( )
| 做不到“光盘” | 能做到“光盘” | 合计 | |
| 男 | 45 | 10 | 55 |
| 女 | 25 | 20 | 45 |
| 合计 | 70 | 30 | 100 |
x2=
| n(n11n22n12n21)2 |
| n1*n2*n*1n*2 |
| P(x2≥k) | 0.05 | 0.010 | 0.005 | 0.001 |
| K | 3.841 | 6.635 | 7.879 | 10.828 |
| A、有95%以上的把握认为“该市居民能否做到“光盘”与性别有关 |
| B、有99%以上的把握认为“该市居民能否做到“光盘”与性别有关 |
| C、有99.5%以上的把握认为“该市居民能否做到“光盘”与性别有关 |
| D、性别不同决定了能否做到“光盘” |
一质点沿直线运动,若由始点起经过t秒后的位移为s=
t3+
t2-4t+7,那么速度为0的时刻为( )
| 1 |
| 3 |
| 3 |
| 2 |
| A、0秒 | B、1秒末 |
| C、2秒末 | D、1秒末和2秒末 |
x为实数,[x]表示不超过x的最大整数(如[-1.5]=-2,[0]=0,[2.3]=2),则关于函数f(x)=x-[x],x∈R的说法不正确的是( )
| A、函数不具有奇偶性 | ||||
| B、x∈[1,2)时函数是增函数 | ||||
| C、函数是周期函数 | ||||
D、若函数g(x)=f(x)-kx恰有两个零点,则k∈(-∞,-1)∪(
|
在等比数列{an}中,a4=8a1,则公比q的值为( )
| A、2 | B、3 | C、4 | D、8 |
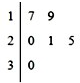 车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则恰有1名优秀工人的概率为
车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则恰有1名优秀工人的概率为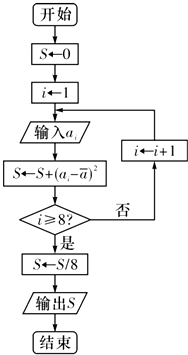 对一个作直线运动的质点的运动过程观测了8次,得到如表所示的数据.
对一个作直线运动的质点的运动过程观测了8次,得到如表所示的数据.