题目内容
x为实数,[x]表示不超过x的最大整数(如[-1.5]=-2,[0]=0,[2.3]=2),则关于函数f(x)=x-[x],x∈R的说法不正确的是( )
| A、函数不具有奇偶性 | ||||
| B、x∈[1,2)时函数是增函数 | ||||
| C、函数是周期函数 | ||||
D、若函数g(x)=f(x)-kx恰有两个零点,则k∈(-∞,-1)∪(
|
考点:抽象函数及其应用
专题:函数的性质及应用
分析:画出函数f(x)=x-[x]的图象如图,据图可知
解答:
 解:作出函数f(x)=x-[x],x∈R的图象,对于A,据图象可知,函数不具有有奇偶性,故A说法正确;
解:作出函数f(x)=x-[x],x∈R的图象,对于A,据图象可知,函数不具有有奇偶性,故A说法正确;
对于B:据图象可知,x∈[1,2)时是单调递增,∴B说法正确.
对C,∵f(x)=x-[x],
∴f(x+1)=(x+1)-[x+1]=x+1-[x]-1=x-[x]=f(x),
∴f(x)=x-[x]在R上为周期是1的函数.∴C说法正确
于对于D,要使g(x)=f(x)-kx恰有两个零点,只要y=f(x)和y=kx有两个交点即可,
当k<-1时,总有两个交点,当直线y=kx过(2,1)下方,(3,1)上方或过(3,1)时,
即k∈(-∞,-1)∪[
,
)时总有两个交点,故说法D不正确.综上,说法不正确的是D
故答案选D
故选D
 解:作出函数f(x)=x-[x],x∈R的图象,对于A,据图象可知,函数不具有有奇偶性,故A说法正确;
解:作出函数f(x)=x-[x],x∈R的图象,对于A,据图象可知,函数不具有有奇偶性,故A说法正确;对于B:据图象可知,x∈[1,2)时是单调递增,∴B说法正确.
对C,∵f(x)=x-[x],
∴f(x+1)=(x+1)-[x+1]=x+1-[x]-1=x-[x]=f(x),
∴f(x)=x-[x]在R上为周期是1的函数.∴C说法正确
于对于D,要使g(x)=f(x)-kx恰有两个零点,只要y=f(x)和y=kx有两个交点即可,
当k<-1时,总有两个交点,当直线y=kx过(2,1)下方,(3,1)上方或过(3,1)时,
即k∈(-∞,-1)∪[
| 1 |
| 3 |
| 1 |
| 2 |
故答案选D
故选D
点评:本题考查抽象函数的图象画法及其性质的应用,属于中档题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
已知曲线C:y=(ax2+2x+3)ex存在两点处的切线互相平行,则a的取值范围为( )
| A、a>1 | ||
B、a<
| ||
C、a≤
| ||
D、a>1或a<
|
函数f(x)=cos(2x-
)+
sinxcosx+
-
sin2x,下列结论中正确的有( )
①f(x)是以π为最小正周期的周期函数;
②直线x=
是函数f(x)的一条对称轴;
③f(x)在区间(0,
)上是单调增函数;
④f(x)既不是奇函数,也不是偶函数.
| π |
| 4 |
| 2 |
| ||
| 2 |
| 2 |
①f(x)是以π为最小正周期的周期函数;
②直线x=
| 3π |
| 8 |
③f(x)在区间(0,
| π |
| 2 |
④f(x)既不是奇函数,也不是偶函数.
| A、1个 | B、2个 | C、3个 | D、4个 |
已知f(x)的定义域为R,则p:?x∈R,(f(x)+f(-x))•(f(x)-f(-x))=0是q:f(x)为奇函数或偶函数的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
在△ABC中,A=
,C=
,b=2,那么a=( )
| π |
| 6 |
| 7π |
| 12 |
A、
| ||
| B、2 | ||
C、2
| ||
| D、1 |
已知一个几何体的三视图如图所示,则该几何体的体积为( )
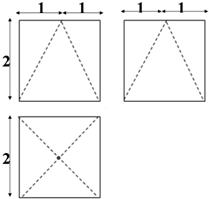

| A、8 | ||
B、
| ||
C、
| ||
| D、4 |
设a>0,b>0,且不等式
+
+
≥0恒成立.则实数k的最小值等于( )
| 1 |
| a |
| 1 |
| b |
| k |
| a+b |
| A、4 | B、0 | C、-2 | D、-4 |
在等差数列{an}中,若a3+a8=24,则S10的值为( )
| A、20 | B、60 | C、90 | D、120 |