题目内容
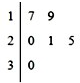 车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则恰有1名优秀工人的概率为
车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则恰有1名优秀工人的概率为考点:茎叶图,古典概型及其概率计算公式
专题:概率与统计
分析:根据茎叶图中的数据,该车间6名工人日加工零件个数的平均值,得出这6名工人中优秀工人数;利用古典概型的概率公式进行计算即可.
解答:
解:根据茎叶图得,该车间6名工人日加工零件个数的平均值是
(17+19+20+21+25+30)=22,
∴这6名工人中优秀工人有2人;
∴从这6名工人中,任取2人,恰有1名优秀工人的概率是
P=
=
.
故答案为:
| 1 |
| 6 |
∴这6名工人中优秀工人有2人;
∴从这6名工人中,任取2人,恰有1名优秀工人的概率是
P=
| ||||
|
| 8 |
| 15 |
故答案为:
| 8 |
| 15 |
点评:本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,则通过该段公路的汽车中,时速在[60,80]的汽车所占比例的估计值为( )
200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,则通过该段公路的汽车中,时速在[60,80]的汽车所占比例的估计值为( )| A、20% | B、40% |
| C、60% | D、80% |
已知
=(2,3,4),
=(6,x,y),若
∥
,则x+y的值是( )
| a |
| b |
| a |
| b |
| A、14 | B、16 | C、21 | D、26 |
已知曲线C:y=(ax2+2x+3)ex存在两点处的切线互相平行,则a的取值范围为( )
| A、a>1 | ||
B、a<
| ||
C、a≤
| ||
D、a>1或a<
|
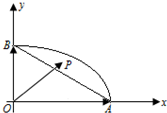 A,B是椭圆的右顶点及上顶点,由椭圆弧
A,B是椭圆的右顶点及上顶点,由椭圆弧