题目内容
已知函数f（x）=
，若f（t）＜f（-t），则t的取值范围是 ．
|
考点：分段函数的应用
专题：综合题,函数的性质及应用
分析：确定函数f（x）的单调性与奇偶性，即可得出结论．
解答：
解：令x＜0，则-x＞0，∴f（-x）=ln（-x），又f（x）=-ln（-x），∴f（-x）=-f（x）；
令x＞0，则-x＜0，∴f（-x）=-ln（x），又f（x）=ln（x），∴f（-x）=-f（x）；
∴f（x）是奇函数，
∵x＞0时，函数单调递增，
∴x＜0时，函数单调递增，
∵f（t）＜f（-t），
∴f（t）＜0
∴0＜t＜1或t＜-1，
∴t的取值范围是0＜t＜1或t＜-1．
故答案为：0＜t＜1或t＜-1．
令x＞0，则-x＜0，∴f（-x）=-ln（x），又f（x）=ln（x），∴f（-x）=-f（x）；
∴f（x）是奇函数，
∵x＞0时，函数单调递增，
∴x＜0时，函数单调递增，
∵f（t）＜f（-t），
∴f（t）＜0
∴0＜t＜1或t＜-1，
∴t的取值范围是0＜t＜1或t＜-1．
故答案为：0＜t＜1或t＜-1．
点评：本题考查了函数的奇偶性与单调性，难度适中，关键是掌握函数的单调性与奇偶性．
练习册系列答案
相关题目
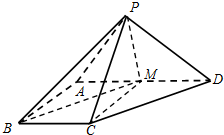如图，四棱锥P-ABCD中，AB⊥AD，AD∥BC，AD=2，AB=BC=1，PA=PD=