题目内容
已知△ABC中，B，C所对的边分别为a，b，c，cosA=
，b=5
，B=
，则a= ．
| 3 |
| 5 |
| 3 |
| π |
| 3 |
考点：余弦定理
专题：三角函数的求值
分析：由cosA的值，利用同角三角函数间的基本关系求出sinA的值，再由b，sinB的值，利用正弦定理即可求出a的值．
解答：
解：∵△ABC中，cosA=
，
∴sinA=
=
，
∵b=5
，B=
，
∴由正弦定理
=
得：a=
=
=8．
故答案为：8
| 3 |
| 5 |
∴sinA=
| 1-cos2A |
| 4 |
| 5 |
∵b=5
| 3 |
| π |
| 3 |
∴由正弦定理
| a |
| sinA |
| b |
| sinB |
| bsinA |
| sinB |
5
| ||||
|
故答案为：8
点评：此题考查了正弦、余弦定理，以及特殊角的三角函数值，熟练掌握定理是解本题的关键．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
新活力总动员暑系列答案
相关题目
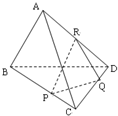（理科）已知如图，四面体ABCD中，P，Q，R分别在棱BC，CD，DA上，且BP=2PC，CQ=2QD，DR=RA，则A，B两点到平面PQR的距离之比为（ ）| A、1：4 | B、1：3 |
| C、1：2 | D、1：1 |
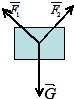甲、乙两位同学参加2014年的自主招生考试，下火车后两人共同提起一个行李包（如图所示）．设他们所用的力分别为