题目内容
设[x]表示不超过x的最大整数,如:[π]=3,[-4.3]=-5.给出下列命题:
①对任意实数x,都有[x]-x≤0;
②若x1≤x2,则[x1]≤[x2];
③[lg1]+[lg2]+[lg3]+…+[lg100]=90;
④若函数f(x)=
-
,则y=[f(x)]+[f(-x)]的值域为{-1,0}.
其中所有真命题的序号是 .
①对任意实数x,都有[x]-x≤0;
②若x1≤x2,则[x1]≤[x2];
③[lg1]+[lg2]+[lg3]+…+[lg100]=90;
④若函数f(x)=
| 2x |
| 1+2x |
| 1 |
| 2 |
其中所有真命题的序号是
考点:命题的真假判断与应用
专题:简易逻辑
分析:直接利用定义判断①②的正误;利用对数值以及新定义求解判断③的正误;先由题意先化简函数f(x)=
-
,通过f(x)与f(-x)的值域讨论,求出f(x)]+[f(-x)]的值,判断④的正误.
| 2x |
| 1+2x |
| 1 |
| 2 |
解答:
解:对于①,对任意实数x,都有[x]-x≤0,满足新定义∴①正确.
对于②,x1≤x2,则[x1]≤[x2],∴②正确.
对于③,[lg1]+[lg2]+[lg3]+[lg4]+…+[lg100]
=0+1×90+2=92,∴③不正确.
对于④,函数f(x)=
-
=
-
∈(-
,
),
同理可得,f(-x)∈(-
,
),
当f(x)∈(-
,0)时,f(-x)∈(0,
),∴[f(x)]=-1,[f(-x)]=0,
∴[f(x)]+[f(-x)]=-1,
同理当f(-x)∈(-
,0)时,f(x)∈(0,
),∴[f(x)]=0,[f(-x)]=-1,
∴[f(x)]+[f(-x)]=-1,
当f(x)=0时,f(-x)=0,∴[f(x)]=0,[f(-x)]=0,
∴[f(x)]+[f(-x)]=0,
综上,y=[f(x)]+[f(-x)]={-1,0}
∴④正确.
故答案为:①②④.
对于②,x1≤x2,则[x1]≤[x2],∴②正确.
对于③,[lg1]+[lg2]+[lg3]+[lg4]+…+[lg100]
=0+1×90+2=92,∴③不正确.
对于④,函数f(x)=
| 2x |
| 1+2x |
| 1 |
| 2 |
| 1 | ||
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
同理可得,f(-x)∈(-
| 1 |
| 2 |
| 1 |
| 2 |
当f(x)∈(-
| 1 |
| 2 |
| 1 |
| 2 |
∴[f(x)]+[f(-x)]=-1,
同理当f(-x)∈(-
| 1 |
| 2 |
| 1 |
| 2 |
∴[f(x)]+[f(-x)]=-1,
当f(x)=0时,f(-x)=0,∴[f(x)]=0,[f(-x)]=0,
∴[f(x)]+[f(-x)]=0,
综上,y=[f(x)]+[f(-x)]={-1,0}
∴④正确.
故答案为:①②④.
点评:本题考查命题的真假的判断,反例法以及新定义的应用是解题的关键,通过取整函数来建立新函数,进而研究其定义域和值域.

练习册系列答案
相关题目
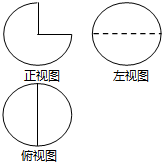 一个几何体的三视图如图所示,其中俯视图与左视图均为半径是2的圆,则这个几何体的表面积是
一个几何体的三视图如图所示,其中俯视图与左视图均为半径是2的圆,则这个几何体的表面积是